Introducción. Paqute qutib

QuTiP es un software de código abierto para simular la dinámica de sistemas cuánticos abiertos. La biblioteca QuTiP depende de los excelentes paquetes numéricos Numpy , Scipy y Cython . Además, Matplotlib proporciona salida gráfica. El lector puede encontrar la web oficial de este paquete en https://qutip.org/. Este paquete dispone de muchas herramientas para poder ser utiliadas por la programación cuántica, pero en este apartado nos vamos a centrar en la posibilidad que ofrece para obtener las posiciones de un vector de estado en la esfera de Bloch. Se instala de la siguiente manera (NOTA: eleiminar el símbolo de comentario para su instalación efectiva):

#!pip install qutip

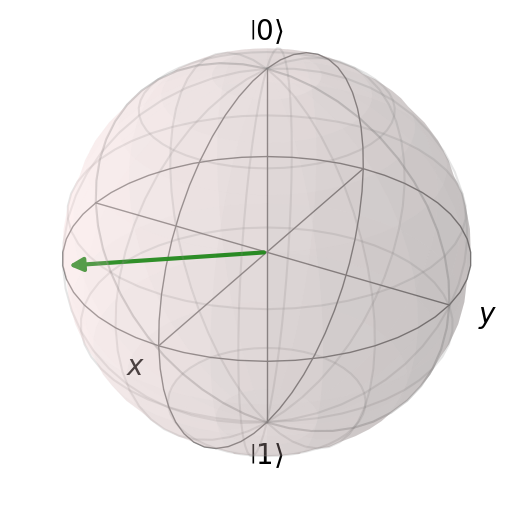
Supongamos que tenemos el siguiente qubit : $\(\frac{\sqrt{3}}{2}|0\rangle-\frac{1}{2}|1\rangle \)

Entonces podemos dibujarlo en la esfera de Bloch de la siguiente manera$

import qutip as qt
import numpy as np

# Ver https://stackoverflow.com/questions/59884561/how-to-plot-a-state-vector-in-bloch-sphere-on-qutip
#Añadimos un estado
state = qt.Qobj(1/2*np.array([np.sqrt(3),-1]))

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[2], line 1
----> 1 import qutip as qt
      2 import numpy as np
      4 # Ver https://stackoverflow.com/questions/59884561/how-to-plot-a-state-vector-in-bloch-sphere-on-qutip
      5 #Añadimos un estado

ModuleNotFoundError: No module named 'qutip'

b = qt.Bloch()
b.add_states(state)
b.show()

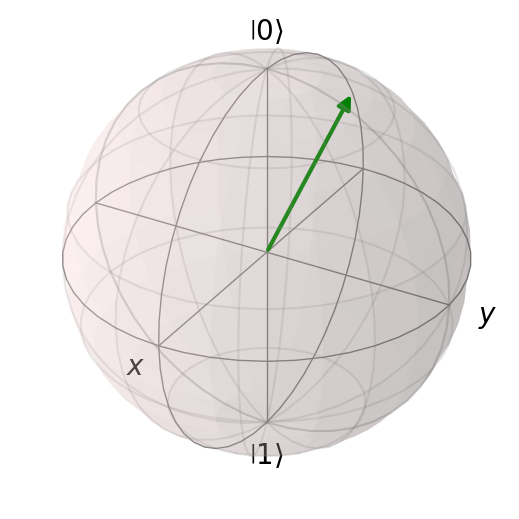
# POdemos dibujar este otro estado
state = qt.Qobj(1/np.sqrt(2)*np.array([1,1]))
b.add_states(state)
b.show()

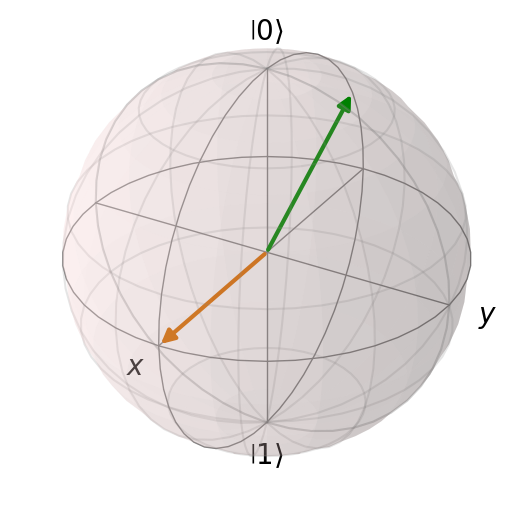
# podemos eliminar todas las representaciones anteriores de la siguiente manera.
b.clear()
b.show()

En un tema anterior, ya hemos visto que el qubit \(\frac{2}{3}|0\rangle+\frac{1-2i}{3}|1\rangle\) perfectamente cumple los requisitos para poder ser considerado como un qubit. A continuación mostramos, el código necesario para su representación en la esfera de Bloch.

# definimos el primer número complejo
z1 = complex(2/3,0)


# Definimos el segundo número complejo
z2 = (1-2j)*(1/3)

state = qt.Qobj(np.array([z1,z2]))
b.add_states(state)
b.show()