7. Introducción#
Vamos a utilizar este apartado para dar una ligeras pinceladas sobre una primera aproximación ak uso de qiskit para trabajar en el mundo de la programación cuántica.
La página oficial de qiskit la podemos encontrar fácilmente en esta dirección web . En este sitio web podemos encontrar muchísima información que nos ayudará a comprender cómo utilizar esta herramienta, aunque bien es cierto que quizá la curva de aprendizaje sea un poquito empinada.
Esta herramienta de desarrollo de software ha sido creada por IBM con la finalidad de trabajar con computadoras cuánticas a nivel de circuitos, pulsos y algoritmos. Con este conjunto de elementos se pueden crear y manipular programas cuánticos y ejecutarlos en dispositivos cuánticos prototipo de IBM Quantum Experience o en simuladores de una computadora local.
Esta plataforma tiene un riquísimo ecosistema constuido por una gran cantidad de plataforma que se <a href=”https://qiskit.github.io/ecosystem/ target=”_blank”> pueden encontrar en este enlace . Dos elementos más oídos de este amplísimo ecosistema son Terra y Aer que junto con otros que se pueden ver en este enlace , constituyen un amplísimo elenco de herramientas para poder trabajar dentro del mundo cuántico.
Entramos en materia viendo algunos de los elementos que se deben importar para tarabajar con este paquete de sofware ( existen muchos más elementos en esta librería que constituyen su API y que el lector puede encontrar en este enlace ).
from qiskit import QuantumCircuit, assemble, Aer
from qiskit.visualization import plot_histogram
7.1. qiskit_textbook#
Dentro de las muchas utilidade de aprendizaje que nos ofrecen en la plataforma qiskit, se encuentra qiskit_textbook, que en el momento de redactar estas lineas lo tienen emplazado en esta dirección web: https://learning.quantum.ibm.com/
NOTA: El paquete qiskit_textbook no se instala directamente con qiskit, es preciso instalarlo de la siguiente manera, pero ojo, antes hay que tener instalado git en la computadora y añadir en la variable patch de las variables de entorno donde está instalado el programa git.exe.
Para ver más sobre esta materia visitar este enlace https://qiskit.org/textbook/ch-prerequisites/setting-the-environment.html
#!pip install git+https://github.com/qiskit-community/qiskit-textbook.git #subdirectory=qiskit-textbook-src
Es de advertir que en el momento de escribir este apartado, IBM está en proceso de modificación de la herramienta de aprendidaje qiskit_textbook, y si entramos en su antigüa dirección web ( https://qiskit.org/textbook/widgets-index.html ), en ella ya se nos indica una nueva dirección más actualizada que se encuentra en <a href=”https://learning.quantum.ibm.com/” target=”_blank”) https://learning.quantum.ibm.com/ .
En la nueva dirección y en el partado titulado *Tools se nos presenta las dos plataformas siguientes:
Quantum Composer, el cual sirve para construir, simular y ejecutar circuitos con una interfat del tipo drag-and-drop
Quantum lab, que nos facilita un entorno de jupyter lab con todos los módulos cargados para poder trabajar directamente con las herramientas implementadas en esta plataforma.
A continuación mostramos un pequeño widget sobre cómo intercambiar información entre números decimales y binarios.
from qiskit_textbook.widgets import binary_widget
binary_widget(nbits=5)
Una de la herramientas muy útiles dentro del mundo Python es poder incorporar latex en las salidas correpondientes. Para esto se suele utilizar el paquete pylatexenc y su instalación se puede hacer desde pip, con una instrucción similar a la que sigue (se debe descomentar si el lector la quiere instalar en su equipo).
#!pip install pylatexenc
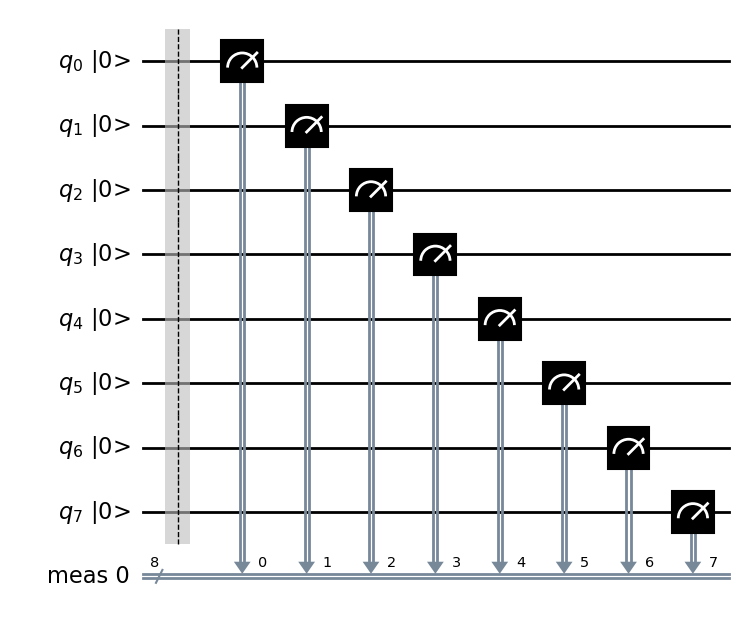
Para irnos familiarizando con la construcción de circuitos, a continuación se muestra en código sencilla que crea un circuito cuántico muy sencillo, constituido por 8 qubits y que simplemente lo que hace es una medición de los mismos. Posteriormente con la tercera línea de código, se procede a mostrar el circuito. Se le añade initial_state=True para que se muestren los estados iniciales, y output=’mpl’ para obtener una salidad gráfica más estética, utilizando para ello el paquete matplotlib.
qc_output = QuantumCircuit(8)
qc_output.measure_all()
qc_output.draw(initial_state=True, output='mpl')
D:\programas\Anaconda\Lib\site-packages\qiskit\visualization\circuit\matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
self._style, def_font_ratio = load_style(self._style)
El código siguiene necesita tener instalado qiskit-aer ( se puede ver en este enlace), lo podemos hacer con el código siguiente:
#!pip install qiskit-aer
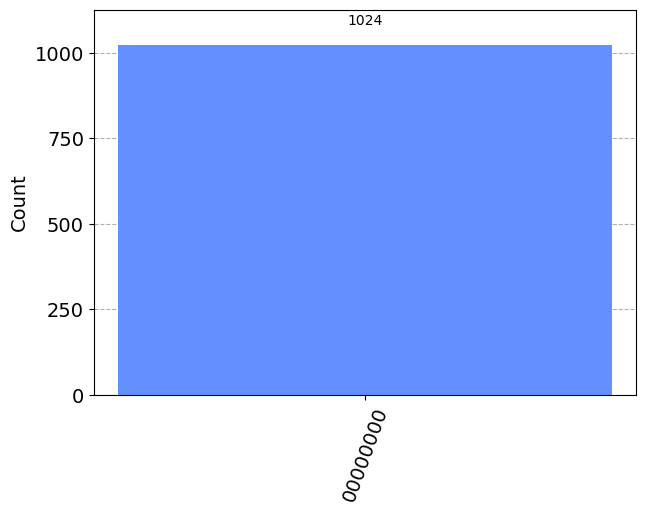
Como la programación cuántica, a diferencia de la tradicional opera mediante probabilidades, lo que suele hacerse en ejecutar el circuito una serie de veces y ver hacia qué estado colapsa en cada medición. Por defecto, la ejecución del circuito se hace un total de 1024 veces, y en uestro caso, como no hemos añadido ninguna puerta cuántica, pues el resultado que se obtiene es siempre el mismo, es decir el estado inicial del que se parte. Esto se suele obtener utilizando un diagrama de barras mediante el comando plot_histogram.
sim = Aer.get_backend('aer_simulator')
result = sim.run(qc_output).result()
counts = result.get_counts()
plot_histogram(counts)
C:\Users\Francisco\AppData\Local\Temp\ipykernel_224\3980966186.py:1: DeprecationWarning: The 'qiskit.Aer' entry point is deprecated and will be removed in Qiskit 1.0. You should use 'qiskit_aer.Aer' directly instead.
sim = Aer.get_backend('aer_simulator')
Veamos el contenido del resultado, almacenado en la variable counts
counts
{'00000000': 1024}
Como puede verse el resultado se obtiene en un diccionario de Python, donde el índice es la composición de estados hacia la que colapsa, y el valor es el número de veces que colapsa hacia ese ese estado.
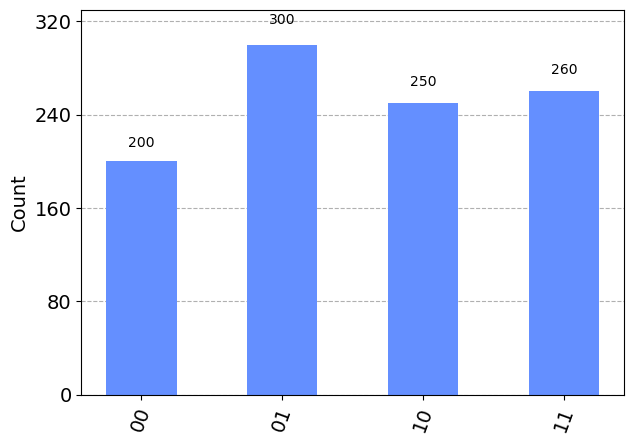
Una simulación de esta situación lo podemos recrear mediante el siguiente código, donde creamos un diccionario conteniendo los cuatro estados posibles de una base al trabajar con dos qubits, e indicando el núemro de veces que se obtienen esos resultados. La representación gráfica también se muestra a continuación del código.
resul={'00':200,'01':300,'10':250,'11':260}
plot_histogram(resul)
7.2. Elementos básicos de qiskit.#
Vamos a continuar en este apartado estudiando y conociendo algunas de las herramientas que podemos utilizar con qiskit. Vamos a trabajar con dos qubits y les vamos a aplicar una puerta de H y una CNOT. Lo hacemos de la siguiente manera
from qiskit import QuantumCircuit
import qiskit.quantum_info as qi
# creamos el circuito con dos qubits
qc_AB = QuantumCircuit(2)
#aplicamos una puerta h
qc_AB.h(0)
# Aplicamos una puerta CNOT
qc_AB.cx(0,1)
qc_AB.draw('mpl')
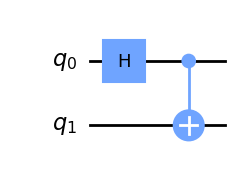
Una vez construido el circuito, podemos obtener el vector de estado del mismo, utilizando el método Statevector.from_instruction() del paqute qiskit.quantum_info:
psi_AB = qi.Statevector.from_instruction(qc_AB)
psi_AB.draw('latex', prefix='|\\psi_{AB}\\rangle = ')
Como puede verse, esta es la manera de poder obtener el primer estado de Bell, que como ya sabemos es un estado entrelazado muy utilizado en la programación cuántica.
7.2.1. Obtención de la matriz de densidad (density matrix).#
La matriz de densidad no es otra cosa más que el producto externo (outer product) de un estado por sí mismo. Por lo tanto, si estamos tabajando sobre n qubits, la matriz de densidad sería una matriz de tamaño \(2^{n}\).
Es decir:
\(\rho=\left[\begin{array}{c} \alpha_{0}\\ \alpha_{1}\\ \vdots\\ \alpha_{n-1} \end{array}\right]\left[\begin{array}{cccc} \alpha_{0}^{*} & \alpha_{1}^{*} & \cdots & \alpha_{n-1}^{*}\end{array}\right]\)
En nuestro caso concreto tendremos:
La forma de obtener este mismo resultado con qiskit es la siguiente:
rho_AB = qi.DensityMatrix.from_instruction(qc_AB)
rho_AB.draw('latex', prefix='\\rho_{AB} = ')
La matriz de densidad la podemos representar de forma gráfica, mediante la clase plot_state_city
from qiskit.visualization import plot_state_city
plot_state_city(rho_AB.data, title='Density Matrix')
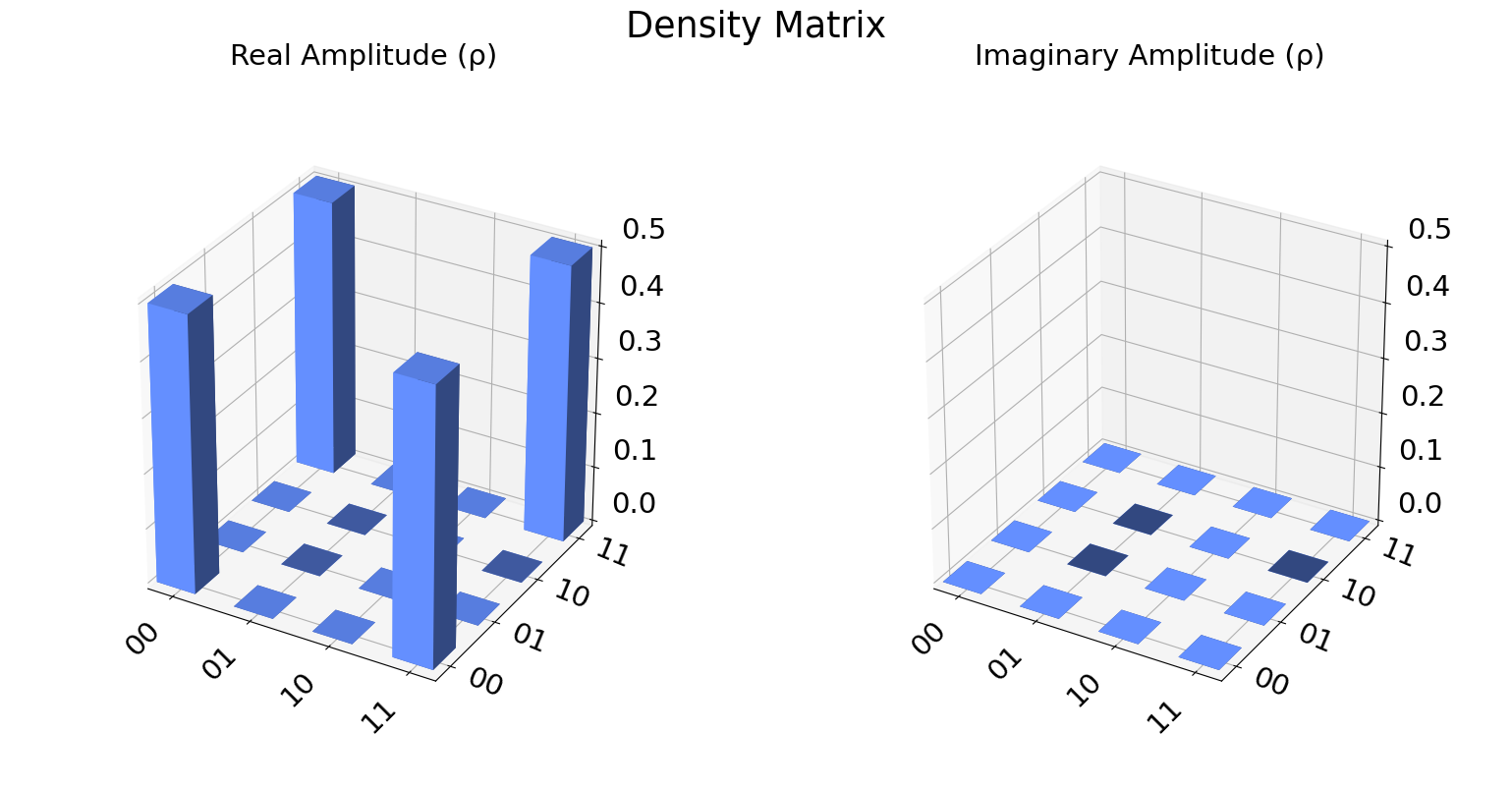
A continuación vamos a aplicar de forma práctica lo visto anteriormente.
Vamos a suponer que tenemos los siguientes estados cuánticos
1.- \({\frac{1}{\sqrt{2}}}{\Big(}|0\rangle-i|1\rangle{\Big)}\)
2.- \({\textstyle\frac{1}{2}}(|00\rangle+|01\rangle+|10\rangle+|11\rangle)\)
Veamos primero el caso 1.
Definimos el vector de estado de la siguiente manera
from numpy import sqrt
sv=qi.Statevector([1/sqrt(2), (0-1j)/sqrt(2)])
sv.draw('latex', prefix='|\\psi_{AB}\\rangle = ')
# calculamos la matriz de densidad
rho_AB = qi.DensityMatrix(sv)
rho_AB.draw('latex', prefix='\\rho_{AB} = ')
plot_state_city(rho_AB.data, title='Density Matrix')
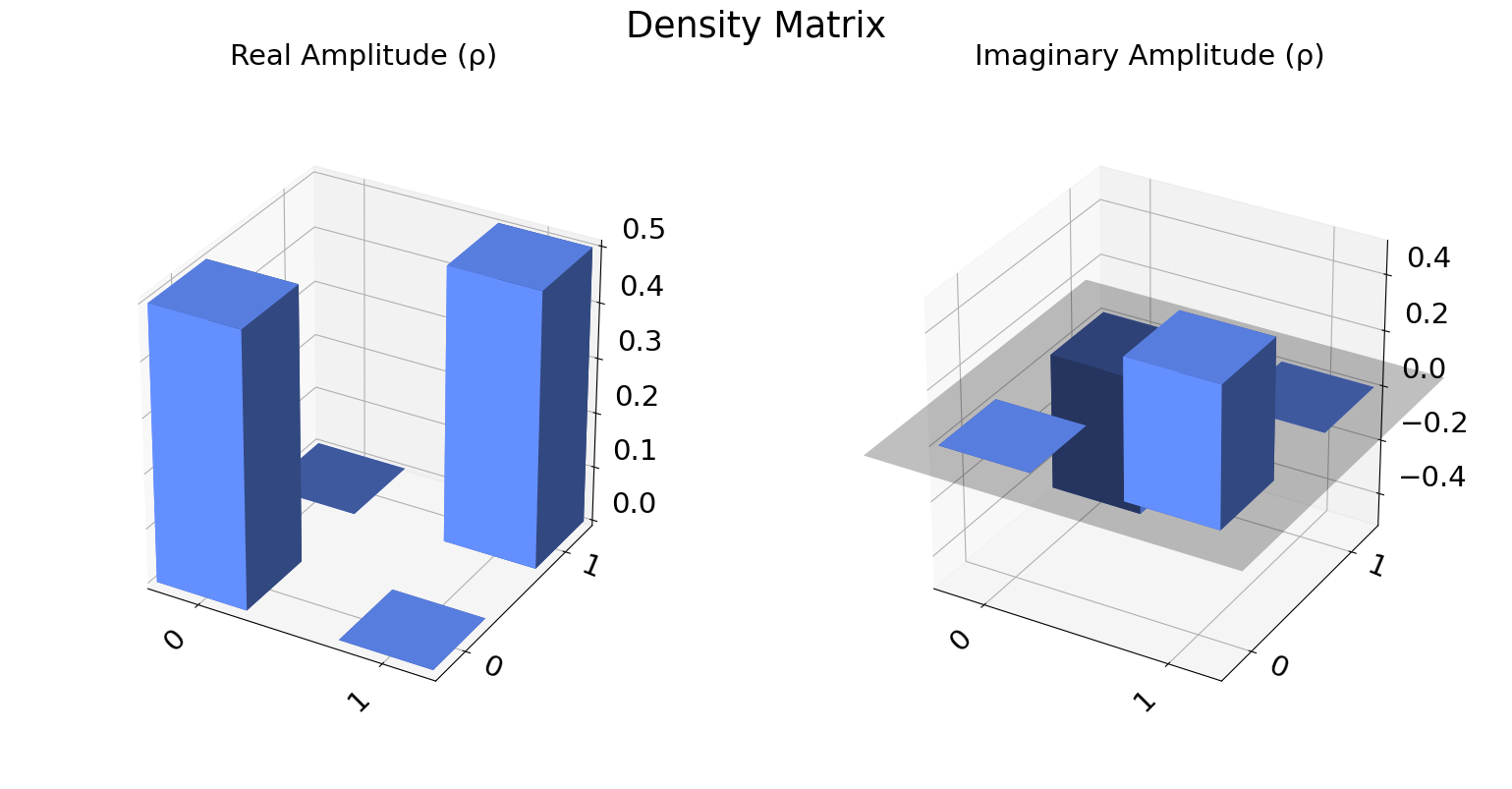
Veamos ahora el segundo caso.
sv=qi.Statevector([1/2,1/2,1/2,1/2])
sv.draw('latex', prefix='|\\psi_{AB}\\rangle = ')
# calculamos la matriz de densidad
rho_AB = qi.DensityMatrix(sv)
rho_AB.draw('latex', prefix='\\rho_{AB} = ')
plot_state_city(rho_AB.data, title='Density Matrix')
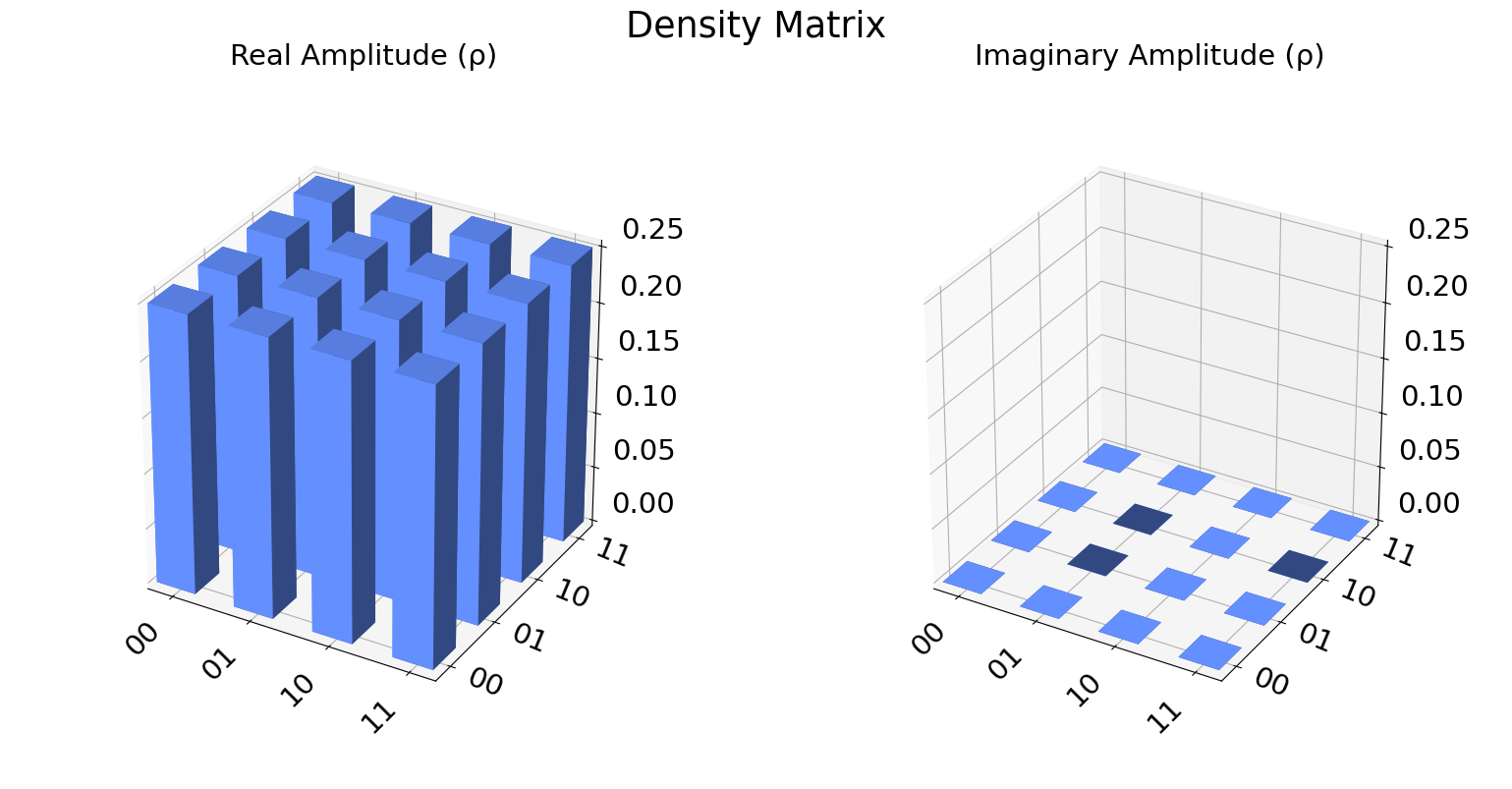
7.3. Creando circuitos básicos#
En este apartado vamos a iniciar a crear un circuito muy básico con qiskit a fin de que el lector vaya tomando contacto con esta posibilidad tan importante que ofrece qiskit.
Comenzamos cargando algunas librerías necesaria
import numpy as np
from qiskit import *
# Creamos un circuito de dos qubits
circ = QuantumCircuit(2)
# Le añadimos una puerta de Hadamard y otra CNOT
circ.h(0)
circ.cx(0,1)
<qiskit.circuit.instructionset.InstructionSet at 0x184bd1df9d0>
7.3.1. Visualizando circuitos#
Utilizaremos matplotlib para ver el circuito que acabamos de crear
circ.draw('mpl')

El circuito anterior, nos va a generar un estado cuánticoigual a
Veámoslo con las siguientes lineas de código
from qiskit.quantum_info import Statevector
state = Statevector.from_int(0,2**2)
state = state.evolve(circ)
state.draw('latex')
# Otra forma alternativa de representación las amplitudes
from qiskit.visualization import array_to_latex
array_to_latex(state)
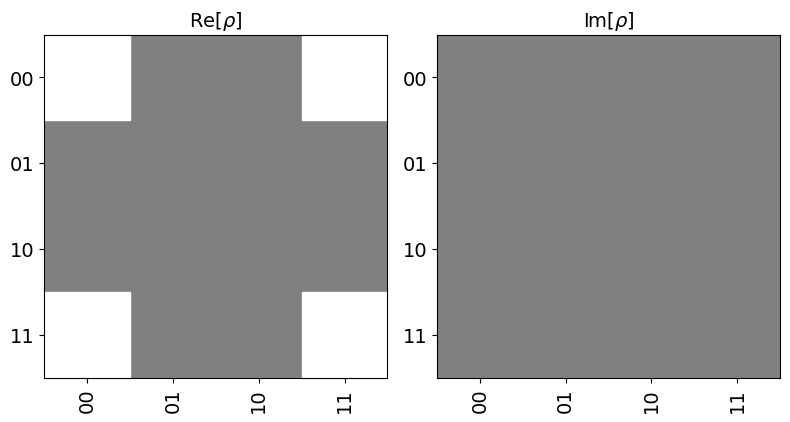
Qiskit nos permite hacer representaciones gráficas de los qubits, a continuación mostramos dos de ellas. La primera es la representación sobre una esfera de Bloch y la segunda la denominada hinton
state.draw('qsphere')
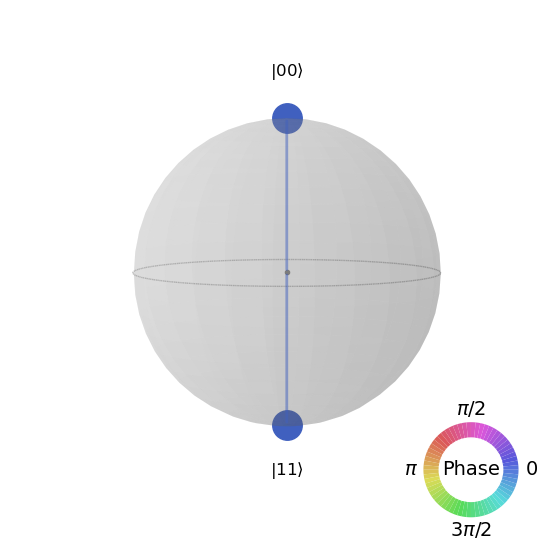
state.draw('hinton')
Igualmente se puede obtener la matriz unitaria de la composición anterior, de la siguiente manera
from qiskit.quantum_info import Operator
U = Operator(circ)
U.data
array([[ 0.70710678+0.j, 0.70710678+0.j, 0. +0.j,
0. +0.j],
[ 0. +0.j, 0. +0.j, 0.70710678+0.j,
-0.70710678+0.j],
[ 0. +0.j, 0. +0.j, 0.70710678+0.j,
0.70710678+0.j],
[ 0.70710678+0.j, -0.70710678+0.j, 0. +0.j,
0. +0.j]])
7.3.2. qiskit Aer#
Qiskit Aer es un paquete para simular circuitos cuánticos y contiene muchos backends para hacer este tipo de simulaciones. Pero hay uno básico que viene con la distribución de Terra denominado BasicAer que vamos a utilizar a continuación para calcular el vector de estado o la matriz unitaria.
7.3.2.1. Backend del vector de estado#
Veamos esta forma de conseguir el vector de estado de circuito anterior.
from qiskit import Aer
backend = Aer.get_backend('statevector_simulator')
job=backend.run(circ)
result = job.result()
vectorEstado = result.get_statevector(circ, decimals=2)
print(vectorEstado)
Statevector([0.71+0.j, 0. +0.j, 0. +0.j, 0.71+0.j],
dims=(2, 2))
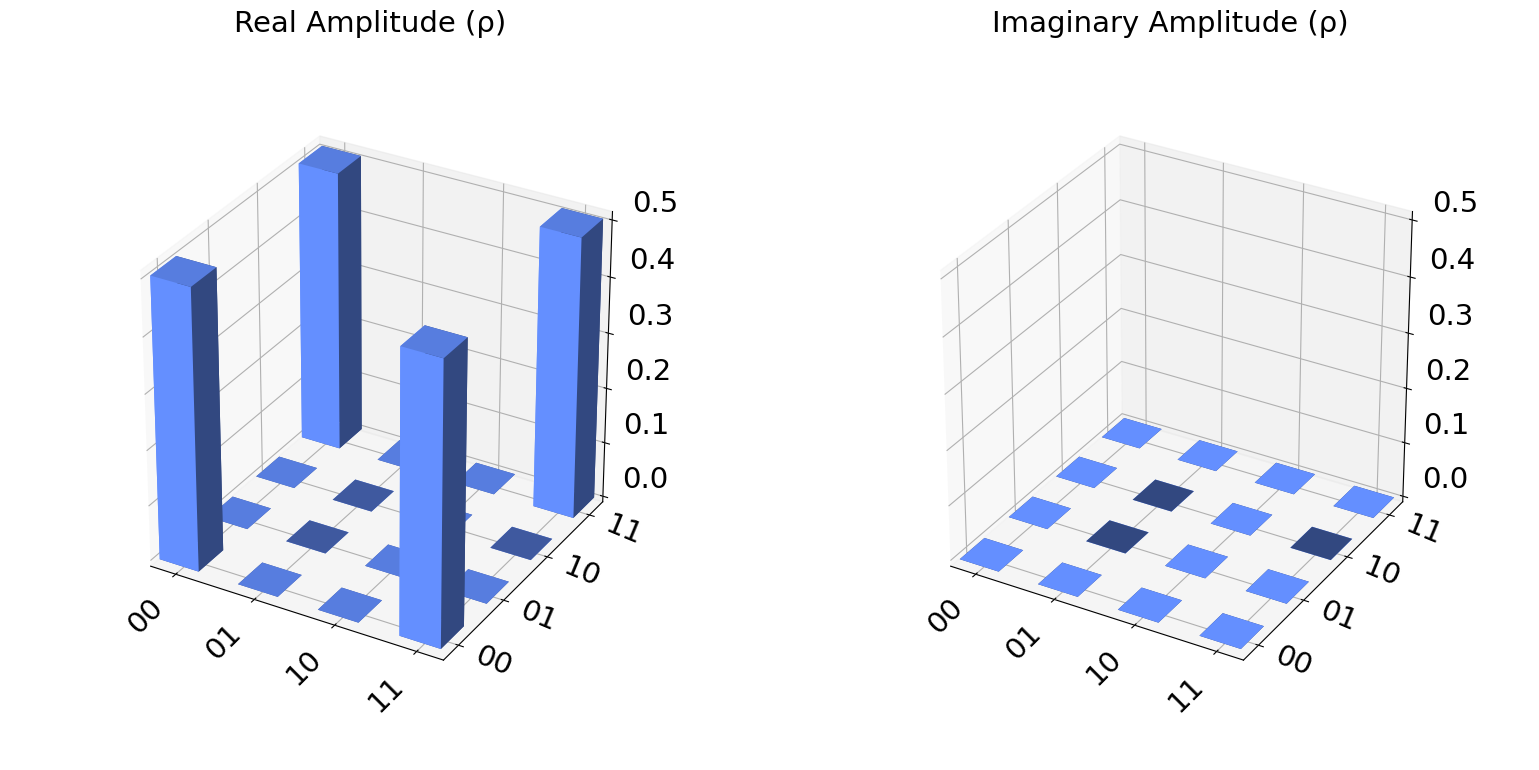
from qiskit.visualization import plot_state_city
plot_state_city(vectorEstado)
7.3.2.2. Backend de la matriz unitaria#
Obtengamos la matriz unitaria de esta composición
backend = Aer.get_backend('unitary_simulator')
job = backend.run(circ)
result = job.result()
print(result.get_unitary(circ, decimals=3))
Operator([[ 0.707+0.j, 0.707-0.j, 0. +0.j, 0. +0.j],
[ 0. +0.j, 0. +0.j, 0.707+0.j, -0.707+0.j],
[ 0. +0.j, 0. +0.j, 0.707+0.j, 0.707-0.j],
[ 0.707+0.j, -0.707+0.j, 0. +0.j, 0. +0.j]],
input_dims=(2, 2), output_dims=(2, 2))
7.3.2.3. Backend OpenQASM#
Obtengamos ahora los resultados de medir las proyecciones sobre los elementos de la base. Para conseguir esta información, debemos añadir alguna instrucción al código anterior, para al final poder hacer una medición del circuito.
circ = QuantumCircuit(2,2)
circ.h(0)
circ.cx(0,1)
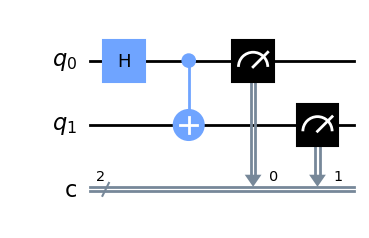
circ.measure(range(2),range(2))
circ.draw('mpl')
D:\programas\Anaconda\Lib\site-packages\qiskit\visualization\circuit\matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
self._style, def_font_ratio = load_style(self._style)
backend_sim = Aer.get_backend('qasm_simulator')
job_sim = backend_sim.run(transpile(circ, backend_sim), shots=1024)
result_sim = job_sim.result()
counts = result_sim.get_counts(circ)
print(counts)
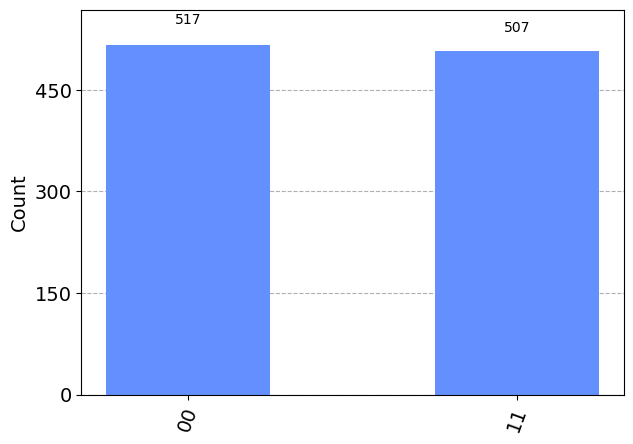
{'00': 517, '11': 507}
from qiskit.visualization import plot_histogram
plot_histogram(counts)
También se puede utilizar AerSimulator del paquete Aer para conseguir esta información
from qiskit.providers.aer import AerSimulator
backend = AerSimulator()
qc_compiled = transpile(circ, backend)
job_sim = backend.run(qc_compiled, shots=1024)
result_sim = job_sim.result()
counts = result_sim.get_counts(qc_compiled)
print(counts)
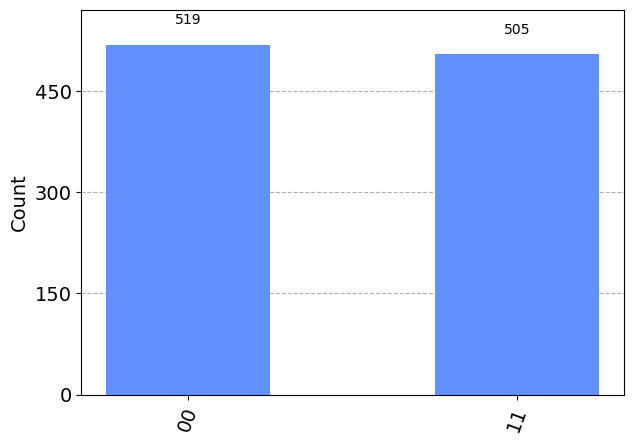
{'11': 505, '00': 519}
C:\Users\Francisco\AppData\Local\Temp\ipykernel_224\607527838.py:1: DeprecationWarning: Importing from 'qiskit.providers.aer' is deprecated. Import from 'qiskit_aer' instead, which should work identically.
from qiskit.providers.aer import AerSimulator
from qiskit.visualization import plot_histogram
plot_histogram(counts)
7.4. Circuito para sumar#
A modo de introducción y con la finalidad de que el lector pueda ver una aplicación práctica de estos circuitos cuánticos, a continuación mostramos un código que sirve para obtener simples sumas.
No es necesario que el lector conozca con detalle lo que se hace en el código anterior, simplemente se expone para que se pueda ver circuitos más complejos en funcionamiento.
# suma de 1+1 en base 2 que es 10 en base dos que es 2 en decimal
qc_ha = QuantumCircuit(4,2)
# encode inputs in qubits 0 and 1
qc_ha.x(0) # For a=0, remove the this line. For a=1, leave it.
qc_ha.x(1) # For b=0, remove the this line. For b=1, leave it.
qc_ha.barrier()
# use cnots to write the XOR of the inputs on qubit 2
qc_ha.cx(0,2)
qc_ha.cx(1,2)
# use ccx to write the AND of the inputs on qubit 3
qc_ha.ccx(0,1,3)
qc_ha.barrier()
# extract outputs
qc_ha.measure(2,0) # extract XOR value
qc_ha.measure(3,1) # extract AND value
qc_ha.draw()
┌───┐ ░ ░
q_0: ┤ X ├─░───■─────────■───░───────
├───┤ ░ │ │ ░
q_1: ┤ X ├─░───┼────■────■───░───────
└───┘ ░ ┌─┴─┐┌─┴─┐ │ ░ ┌─┐
q_2: ──────░─┤ X ├┤ X ├──┼───░─┤M├───
░ └───┘└───┘┌─┴─┐ ░ └╥┘┌─┐
q_3: ──────░───────────┤ X ├─░──╫─┤M├
░ └───┘ ░ ║ └╥┘
c: 2/═══════════════════════════╩══╩═
0 1 # suma de 0+1 en base 2 que es 1 o 01
qc_ha = QuantumCircuit(4,2)
# encode inputs in qubits 0 and 1
#qc_ha.x(0) # For a=0, remove the this line. For a=1, leave it.
qc_ha.x(1) # For b=0, remove the this line. For b=1, leave it.
qc_ha.barrier()
# use cnots to write the XOR of the inputs on qubit 2
qc_ha.cx(0,2)
qc_ha.cx(1,2)
# use ccx to write the AND of the inputs on qubit 3
qc_ha.ccx(0,1,3)
qc_ha.barrier()
# extract outputs
qc_ha.measure(2,0) # extract XOR value
qc_ha.measure(3,1) # extract AND value
qc_ha.draw()
░ ░
q_0: ──────░───■─────────■───░───────
┌───┐ ░ │ │ ░
q_1: ┤ X ├─░───┼────■────■───░───────
└───┘ ░ ┌─┴─┐┌─┴─┐ │ ░ ┌─┐
q_2: ──────░─┤ X ├┤ X ├──┼───░─┤M├───
░ └───┘└───┘┌─┴─┐ ░ └╥┘┌─┐
q_3: ──────░───────────┤ X ├─░──╫─┤M├
░ └───┘ ░ ║ └╥┘
c: 2/═══════════════════════════╩══╩═
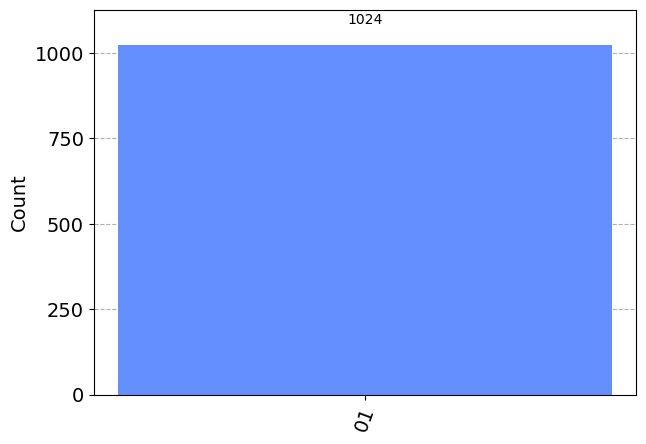
0 1 #qobj = assemble(qc_ha)
sim = Aer.get_backend('aer_simulator')
counts = sim.run(qc_ha).result().get_counts()
#counts = sim.run(qobj).result().get_counts()
plot_histogram(counts)
# suma de 1+0 en base 2 que es 1
qc_ha = QuantumCircuit(4,2)
# encode inputs in qubits 0 and 1
qc_ha.x(0) # For a=0, remove the this line. For a=1, leave it.
#qc_ha.x(1) # For b=0, remove the this line. For b=1, leave it.
qc_ha.barrier()
# use cnots to write the XOR of the inputs on qubit 2
qc_ha.cx(0,2)
qc_ha.cx(1,2)
# use ccx to write the AND of the inputs on qubit 3
qc_ha.ccx(0,1,3)
qc_ha.barrier()
# extract outputs
qc_ha.measure(2,0) # extract XOR value
qc_ha.measure(3,1) # extract AND value
qc_ha.draw()
┌───┐ ░ ░
q_0: ┤ X ├─░───■─────────■───░───────
└───┘ ░ │ │ ░
q_1: ──────░───┼────■────■───░───────
░ ┌─┴─┐┌─┴─┐ │ ░ ┌─┐
q_2: ──────░─┤ X ├┤ X ├──┼───░─┤M├───
░ └───┘└───┘┌─┴─┐ ░ └╥┘┌─┐
q_3: ──────░───────────┤ X ├─░──╫─┤M├
░ └───┘ ░ ║ └╥┘
c: 2/═══════════════════════════╩══╩═
0 1 #qobj = assemble(qc_ha)
sim = Aer.get_backend('aer_simulator')
#counts = sim.run(qobj).result().get_counts()
counts = sim.run(qc_ha).result().get_counts()
plot_histogram(counts)
