12. Explorando la puerta CNOT-Gate

En la sección anterior, vimos algunos resultados muy básicos con la puerta CNOT. Aquí exploraremos algunos resultados más interesantes. .

Vimos que podíamos entrelazar los dos qubits colocando el qubit de control en el estado \(|+\rangle\):

\[ \text{CNOT}|0{+}\rangle = \tfrac{1}{\sqrt{2}}(|00\rangle + |11\rangle) \]

Pero, ¿qué ocurre si ponemos el segundo qubit en superposición?

Veamos el resultado anterior con qiskit

from qiskit import QuantumCircuit, Aer, assemble
from math import pi
import numpy as np
from qiskit.visualization import plot_bloch_multivector, plot_histogram, array_to_latex

qc = QuantumCircuit(2)
qc.h(1) # convierto qubit 1 en X
qc.cx(1,0)
qc.draw(output='mpl')

D:\programas\Anaconda\Lib\site-packages\qiskit\visualization\circuit\matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
  self._style, def_font_ratio = load_style(self._style)

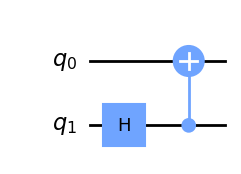
# Let's see the result
svsim = Aer.get_backend('aer_simulator')
qc.save_statevector()
qobj = assemble(qc)
final_state = svsim.run(qobj).result().get_statevector()
display(array_to_latex(final_state, prefix="\\text{Statevector} = "))

C:\Users\Francisco\AppData\Local\Temp\ipykernel_18892\3758938065.py:2: DeprecationWarning: The 'qiskit.Aer' entry point is deprecated and will be removed in Qiskit 1.0. You should use 'qiskit_aer.Aer' directly instead.
  svsim = Aer.get_backend('aer_simulator')
C:\Users\Francisco\AppData\Local\Temp\ipykernel_18892\3758938065.py:5: DeprecationWarning: Using a qobj for run() is deprecated as of qiskit-aer 0.9.0 and will be removed no sooner than 3 months from that release date. Transpiled circuits should now be passed directly using `backend.run(circuits, **run_options).
  final_state = svsim.run(qobj).result().get_statevector()

\[\begin{split} \text{Statevector} = \begin{bmatrix} \frac{\sqrt{2}}{2} & 0 & 0 & \frac{\sqrt{2}}{2} \\ \end{bmatrix} \end{split}\]

Veamos ahora otro estado

qc = QuantumCircuit(2)
qc.h(0)
qc.h(1)
qc.cx(0,1)
qc.draw(output='mpl')

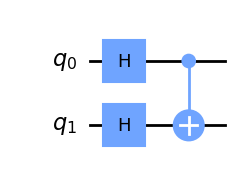
En el circuito anterior, tenemos la CNOT actuando sobre el estado:

\[ |{+}{+}\rangle = \tfrac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) \]

Puesto que CNOT intercambia las amplitudes de \(|01\rangle\) y \(|11\rangle\), no vemos ningún cambio:

qc = QuantumCircuit(2)
qc.h(0)
qc.h(1)
qc.cx(0,1)
display(qc.draw(output='mpl'))  # `display` is a command for Jupyter notebooks
                    # similar to `print`, but for rich content

# Let's see the result
svsim = Aer.get_backend('aer_simulator')
qc.save_statevector()
qobj = assemble(qc)
final_state = svsim.run(qobj).result().get_statevector()
display(array_to_latex(final_state, prefix="\\text{Statevector} = "))
plot_bloch_multivector(final_state)

C:\Users\Francisco\AppData\Local\Temp\ipykernel_18892\4150523781.py:12: DeprecationWarning: Using a qobj for run() is deprecated as of qiskit-aer 0.9.0 and will be removed no sooner than 3 months from that release date. Transpiled circuits should now be passed directly using `backend.run(circuits, **run_options).
  final_state = svsim.run(qobj).result().get_statevector()

\[\begin{split} \text{Statevector} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \end{bmatrix} \end{split}\]

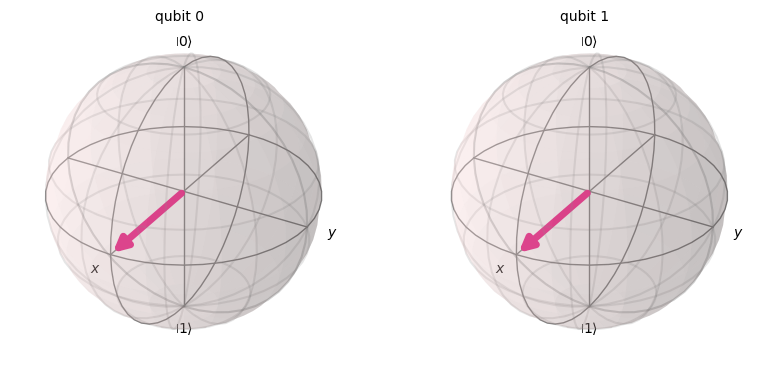
Pongamos el qubit objetivo en el estado \(|-\rangle\), para que tenga una fase negativa:

qc = QuantumCircuit(2)
qc.h(0)
qc.x(1)
qc.h(1)
qc.draw(output='mpl')

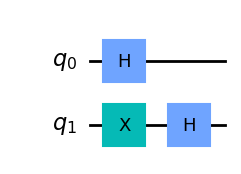
Esto crea el estado:

\[ |{-}{+}\rangle = \tfrac{1}{2}(|00\rangle + |01\rangle - |10\rangle - |11\rangle) \]

qc = QuantumCircuit(2)
qc.h(0)
qc.x(1)
qc.h(1)
display(qc.draw(output='mpl'))
# See the result
qc1 = qc.copy()
qc1.save_statevector()
final_state = svsim.run(qc1).result().get_statevector()
display(array_to_latex(final_state, prefix="\\text{Statevector} = "))
plot_bloch_multivector(final_state)

\[\begin{split} \text{Statevector} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & - \frac{1}{2} & - \frac{1}{2} \\ \end{bmatrix} \end{split}\]

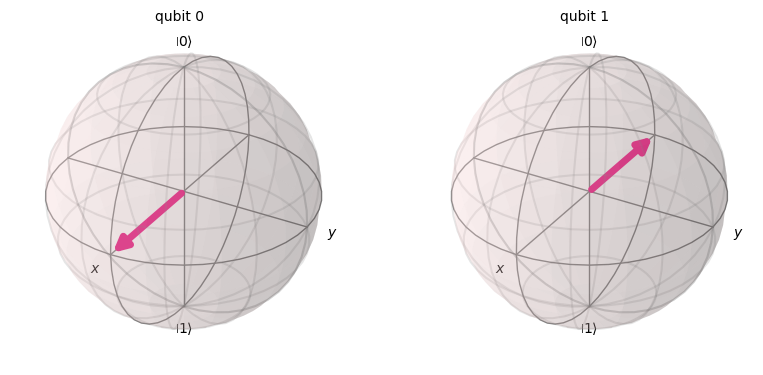
Si el CNOT actúa sobre este estado, intercambiaremos las amplitudes de \(|01\rangle\) y \(|11\rangle\), dando como resultado el estado:

\[\begin{split} \begin{aligned} \text{CNOT}|{-}{+}\rangle & = \tfrac{1}{2}(|00\rangle - |01\rangle - |10\rangle + |11\rangle) \\ & = |{-}{-}\rangle \end{aligned} \end{split}\]

Esto es interesante, porque afecta al estado del qubit control mientras que deja el estado del qubit target sin cambios.

qc.cx(0,1)
display(qc.draw(output='mpl'))

qc.save_statevector()
qobj = assemble(qc)
final_state = svsim.run(qobj).result().get_statevector()
display(array_to_latex(final_state, prefix="\\text{Statevector} = "))
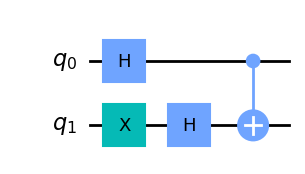
plot_bloch_multivector(final_state)

C:\Users\Francisco\AppData\Local\Temp\ipykernel_18892\686013327.py:6: DeprecationWarning: Using a qobj for run() is deprecated as of qiskit-aer 0.9.0 and will be removed no sooner than 3 months from that release date. Transpiled circuits should now be passed directly using `backend.run(circuits, **run_options).
  final_state = svsim.run(qobj).result().get_statevector()

\[\begin{split} \text{Statevector} = \begin{bmatrix} \frac{1}{2} & - \frac{1}{2} & - \frac{1}{2} & \frac{1}{2} \\ \end{bmatrix} \end{split}\]

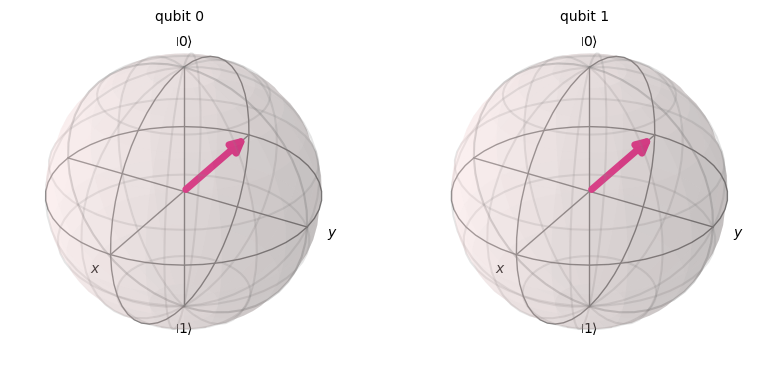
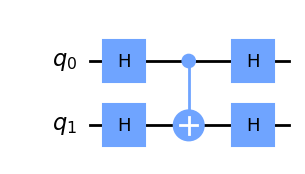
Si recordamos las transformaciones H-gate \(|{+}\rangle \rightarrow |0\rangle\) y \(|{-}\rangle \rightarrow |1\rangle\), podemos ver que envolver un CNOT en H-gates tiene el comportamiento equivalente a un CNOT actuando en la dirección opuesta:

Podemos comprobarlo utilizando el simulador Aer de Qiskit:

qc = QuantumCircuit(2)
qc.h(0)
qc.h(1)
qc.cx(0,1)
qc.h(0)
qc.h(1)
display(qc.draw(output='mpl')) 

qc.save_unitary()
usim = Aer.get_backend('aer_simulator')
qobj = assemble(qc)
unitary = usim.run(qobj).result().get_unitary()
array_to_latex(unitary, prefix="\\text{Circuit = }\n")

C:\Users\Francisco\AppData\Local\Temp\ipykernel_18892\3061567878.py:12: DeprecationWarning: Using a qobj for run() is deprecated as of qiskit-aer 0.9.0 and will be removed no sooner than 3 months from that release date. Transpiled circuits should now be passed directly using `backend.run(circuits, **run_options).
  unitary = usim.run(qobj).result().get_unitary()

\[ \begin{align}\begin{aligned} \text{Circuit = }\\\begin{split}\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \end{split}\end{aligned}\end{align} \]

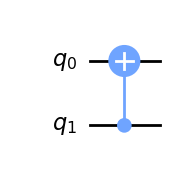
qc = QuantumCircuit(2)
qc.cx(1,0)
display(qc.draw(output='mpl'))
qc.save_unitary()

qobj = assemble(qc)
unitary = usim.run(qobj).result().get_unitary()
array_to_latex(unitary, prefix="\\text{Circuit = }\n")

C:\Users\Francisco\AppData\Local\Temp\ipykernel_18892\661953302.py:7: DeprecationWarning: Using a qobj for run() is deprecated as of qiskit-aer 0.9.0 and will be removed no sooner than 3 months from that release date. Transpiled circuits should now be passed directly using `backend.run(circuits, **run_options).
  unitary = usim.run(qobj).result().get_unitary()

\[ \begin{align}\begin{aligned} \text{Circuit = }\\\begin{split}\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \end{split}\end{aligned}\end{align} \]

Esta identidad es un ejemplo de “retroceso de fase” (phase kickback), lo que nos lleva a la siguiente sección….

13. 2. Phase Kickback

13.1. Explicación de la identidad del circuito CNOT

En la sección anterior vimos esta identidad:

Este es un ejemplo de kickback (o, kickback de fase ) que es muy importante y se utiliza en casi todos los algoritmos cuánticos. Kickback es donde el valor propio añadido por una puerta a un qubit es “devuelto” a un qubit diferente a través de una operación controlada. Por ejemplo, vimos que realizar una puerta-X en un qubit \(|{-}\rangle\) le da la fase \(-1\):

\[ X|{-}\rangle = -|{-}\rangle \]

Cuando nuestro qubit de control está en \(|0\rangle\) o \(|1\rangle\), esta fase afecta a todo el estado, sin embargo es una fase global y no tiene efectos observables:

\[\begin{split} \begin{aligned} \text{CNOT}|{-}0\rangle & = |{-}\rangle \otimes |0\rangle \\ & = |{-}0\rangle \\ \quad & \\ \text{CNOT}|{-}1\rangle & = X|{-}\rangle \otimes |1\rangle \\ & = -|{-}\rangle \otimes |1\rangle \\ & = -|{-}1\rangle \\ \end{aligned} \end{split}\]

El efecto interesante es cuando nuestro qubit de control está en superposición. El componente del qubit de control que se encuentra en la dirección de \(|1\rangle\) aplica este factor de fase al qubit objetivo correspondiente. Este factor de fase aplicado a su vez introduce una fase relativa en el qubit de control:

\[\begin{split} \begin{aligned} \text{CNOT}|{-}{+}\rangle & = \tfrac{1}{\sqrt{2}}(\text{CNOT}|{-}0\rangle + \text{CNOT}|{-}1\rangle) \\ & = \tfrac{1}{\sqrt{2}}(|{-}0\rangle + X|{-}1\rangle) \\ & = \tfrac{1}{\sqrt{2}}(|{-}0\rangle -|{-}1\rangle) \\ \end{aligned} \end{split}\]

Esto se puede escribir como los dos estados de qubit separables:

\[\begin{split} \begin{aligned} \text{CNOT}|{-}{+}\rangle & = |{-}\rangle \otimes \tfrac{1}{\sqrt{2}}(|{0}\rangle - |1\rangle )\\ & = |{-}{-}\rangle \\ \end{aligned} \end{split}\]

colocar el CNOT en las puertas H transforma los qubits de la base computacional a la base \((|+\rangle, |-\rangle)\), donde vemos este efecto. Esta identidad es muy útil en hardware, ya que algunos hardwares sólo permiten CNOTs en una dirección entre dos qubits específicos. Podemos utilizar esta identidad para superar este problema y permitir CNOTs en ambas direcciones.

13.2. 2.2 Kickback con la puerta T-gate

Veamos otra operación controlada, la puerta T controlada:

qc = QuantumCircuit(2)
qc.cp(pi/4, 0, 1)
qc.draw(output='mpl')

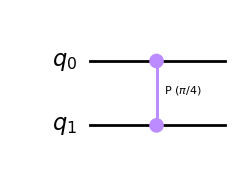
La puerta T-gate tiene la siguiente matriz:

\[\begin{split} \text{T} = \begin{bmatrix} 1 & 0 \\ 0 & e^{i\pi/4}\\ \end{bmatrix} \end{split}\]

Y la puerta T-gate controlada tiene la siguiente matriz:

\[\begin{split} \text{Controlled-T} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & e^{i\pi/4}\\ \end{bmatrix} \end{split}\]

Podemos comprobarlo utilizando el simulador Aer de Qiskit:

qc = QuantumCircuit(2)
qc.cp(pi/4, 0, 1)
display(qc.draw(output='mpl'))
# See Results:
qc.save_unitary()
qobj = assemble(qc)
unitary = usim.run(qobj).result().get_unitary()
array_to_latex(unitary, prefix="\\text{Controlled-T} = \n")

C:\Users\Francisco\AppData\Local\Temp\ipykernel_18892\1088296195.py:7: DeprecationWarning: Using a qobj for run() is deprecated as of qiskit-aer 0.9.0 and will be removed no sooner than 3 months from that release date. Transpiled circuits should now be passed directly using `backend.run(circuits, **run_options).
  unitary = usim.run(qobj).result().get_unitary()

\[ \begin{align}\begin{aligned} \text{Controlled-T} = \\\begin{split}\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & \frac{\sqrt{2}}{2} + \frac{\sqrt{2} i}{2} \\ \end{bmatrix} \end{split}\end{aligned}\end{align} \]

De forma más general, podemos encontrar la matriz de cualquier operación controlada-U utilizando la regla:

\[\begin{split} \begin{aligned} \text{U} & = \begin{bmatrix} u_{00} & u_{01} \\ u_{10} & u_{11}\\ \end{bmatrix} \\ \quad & \\ \text{Controlled-U} & = \begin{bmatrix} I & 0 \\ 0 & U\\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & u_{00} & u_{01} \\ 0 & 0 & u_{10} & u_{11}\\ \end{bmatrix} \end{aligned} \end{split}\]

O, usando la ordenación de qubits de Qiskit:

\[\begin{split} \text{Controlled-U} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & u_{00} & 0 & u_{01} \\ 0 & 0 & 1 & 0 \\ 0 & u_{10} & 0 & u_{11}\\ \end{bmatrix} \end{split}\]

Si aplicamos la puerta T a un qubit en el estado \(|1\rangle\), añadimos una fase de \(e^{i\pi/4}\) a este qubit:

\[ T|1\rangle = e^{i\pi/4}|1\rangle \]

Esto es fase global y es inobservable. Pero si controlamos esta operación usando otro qubit en el estado \(|{+}\rangle\), la fase ya no es global sino relativa, lo que cambia la fase relativa en nuestro qubit de control:

\[\begin{split} \begin{aligned} |1{+}\rangle & = |1\rangle \otimes \tfrac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \\ & = \tfrac{1}{\sqrt{2}}(|10\rangle + |11\rangle) \\ & \\ \text{Controlled-T}|1{+}\rangle & = \tfrac{1}{\sqrt{2}}(|10\rangle + e^{i\pi/4}|11\rangle) \\ & \\ & = |1\rangle \otimes \tfrac{1}{\sqrt{2}}(|0\rangle + e^{i\pi/4}|1\rangle) \end{aligned} \end{split}\]

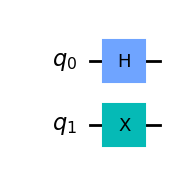
Esto tiene el efecto de rotar nuestro qubit de control alrededor del eje Z de la esfera de Bloch, mientras que deja el qubit objetivo sin cambios. Veamos esto en Qiskit:

qc = QuantumCircuit(2)
qc.h(0)
qc.x(1)
display(qc.draw(output='mpl'))
# See Results:
qc.save_statevector()
qobj = assemble(qc)
final_state = svsim.run(qobj).result().get_statevector()
plot_bloch_multivector(final_state)

C:\Users\Francisco\AppData\Local\Temp\ipykernel_18892\4247561864.py:8: DeprecationWarning: Using a qobj for run() is deprecated as of qiskit-aer 0.9.0 and will be removed no sooner than 3 months from that release date. Transpiled circuits should now be passed directly using `backend.run(circuits, **run_options).
  final_state = svsim.run(qobj).result().get_statevector()

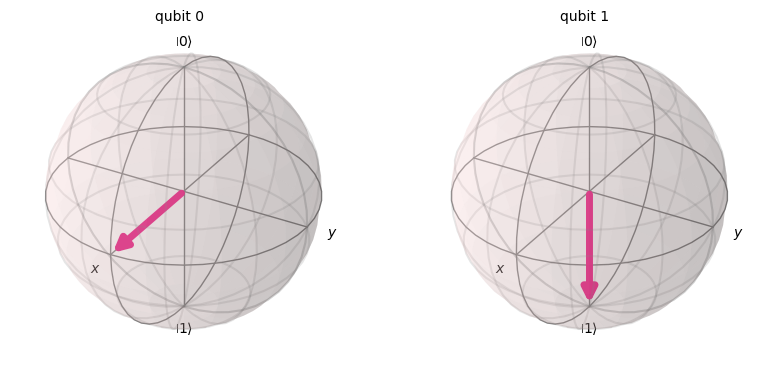
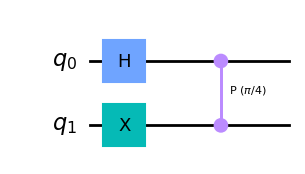
qc = QuantumCircuit(2)
qc.h(0)
qc.x(1)
# Add Controlled-T
qc.cp(pi/4, 0, 1)
display(qc.draw(output='mpl'))
# See Results:
qc.save_statevector()
qobj = assemble(qc)
final_state = svsim.run(qobj).result().get_statevector()
plot_bloch_multivector(final_state)

C:\Users\Francisco\AppData\Local\Temp\ipykernel_18892\2878867670.py:10: DeprecationWarning: Using a qobj for run() is deprecated as of qiskit-aer 0.9.0 and will be removed no sooner than 3 months from that release date. Transpiled circuits should now be passed directly using `backend.run(circuits, **run_options).
  final_state = svsim.run(qobj).result().get_statevector()

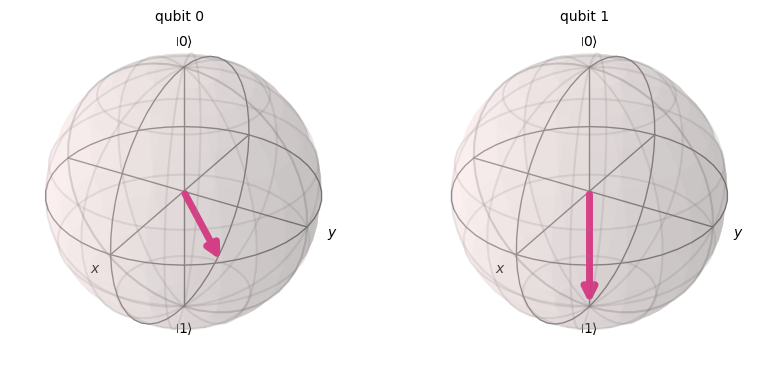
Podemos ver que el qubit más a la izquierda ha sido rotado \(\pi/4\) alrededor del eje Z de la esfera de Bloch, como era de esperar. Después de explorar este comportamiento, puede quedar claro por qué Qiskit dibuja las puertas de rotación Z controlada de esta manera simétrica (dos controles en lugar de un control y un objetivo). No hay un qubit de control o de destino claro para todos los casos.

13.3. Quick Ejercicios:

1. ¿Cuál sería el estado resultante del qubit de control (q0) si el qubit objetivo (q1) estuviera en el estado $|0\rangle$? (como se muestra en el circuito de abajo)? Utiliza Qiskit para comprobar tu respuesta.
   
2. ¿Qué le ocurriría al qubit de control (q0) si el qubit de destino (q1) estuviera en el estado $|1\rangle$, y el circuito utilizara una puerta Sdg controlada en lugar de la T controlada (como se muestra en el circuito de abajo)?
   
3. ¿Qué pasaría con el qubit de control (q0) si estuviera en el estado $|1\rangle$ en lugar del estado $|{+}\rangle$ antes de la aplicación de la T controlada (como se muestra en el circuito de abajo)?
   

import qiskit.tools.jupyter
%qiskit_version_table

C:\Users\Francisco\AppData\Local\Temp\ipykernel_18892\3369625891.py:1: DeprecationWarning: qiskit.tools.jupyter is deprecated and will be removed in Qiskit 1.0.0
  import qiskit.tools.jupyter

Version Information

Software	Version
qiskit	0.46.0
qiskit_aer	0.13.2
System information
Python version	3.11.4
Python compiler	MSC v.1916 64 bit (AMD64)
Python build	main, Jul 5 2023 13:38:37
OS	Windows
CPUs	4
Memory (Gb)	11.799663543701172
Sat Feb 03 21:20:23 2024 Hora estándar romance