28. Introducción.#
En este módulo vamos a utilizar un modelo de optimización de con variables de tipo discreto, aunque realmente las variables van a ser binario (con valores 0 ó 1) a las que añadimos una restricción para que algunas de ellas valgan 1. Eso lo vemos en la exposición de la resolución del problema
En primer lugar creamos la función que va a ser la encargada de generar los puntos que después vamos a clasificar.
import numpy as np
def generate_points(centers, counts, scales):
"""Generamos puntos en un espacio bidimensional
Args:
centers: lista de pares que serán los centros de los cluster
counts: lista conteniendo el número de puntos de cada cluster
scales: Desviación estándar a tener en cuenta para generar los puntos.
Returns:
points: lista de los puntos (con un tamaño igual a la suma del tamaño de cada cluster)
"""
centers = np.array(centers)
points = np.zeros([sum(counts), 2])
start = 0
for center, count, scale in zip(centers, counts, scales):
points[start:start + count] = center + np.random.normal(0, scale, size=[count, 2])
start += count
return points
# tres clusters con 3,4 y 3 puntos cada uno
counts = [3, 4, 3]
num_points = sum(counts)
num_clusters = len(counts)
points = generate_points([(-1, 1), (1, 1), (0, 2)], counts, [0.1, 0.1, 0.1])
# obtenemos la distancia entre cada punto
distances = {(i, j): np.sqrt(np.sum(np.square(points[i] - points[j])))
for i in range(num_points)
for j in range(num_points)
if i != j
}
one_hot_penalty = 10
import matplotlib.pyplot as plt
plt.scatter(*zip(*points))
<matplotlib.collections.PathCollection at 0x1bd964a45b0>
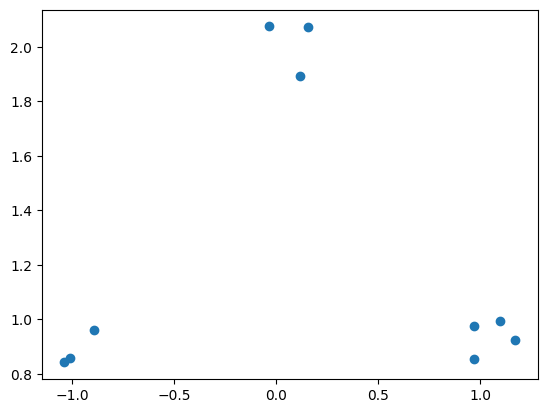
points
array([[-1.01018262, 0.8585598 ],
[-1.03893959, 0.84209375],
[-0.89338935, 0.96061314],
[ 0.96746306, 0.97584494],
[ 1.17195097, 0.9230145 ],
[ 0.96882718, 0.85484122],
[ 1.09785392, 0.99590056],
[ 0.11826868, 1.89123145],
[-0.03513448, 2.07471489],
[ 0.15519415, 2.0729186 ]])
points[1]-points[2]
array([-0.14555024, -0.11851938])
#distances
28.1. Creación del objeto BQM#
Creamos un objeto de tipo BQM con las siguientes características.
La variables de decisión \(x_{ij}\) van a valer 1 si el punto i es asignado al conglomerado j y cero en caso contrario.
El número total de variables será igual al número de clúster multiplicado por el número de puntos.
No hay ninguna incialización de los valores bias puesto que se asignan los mismos valores iniciales a todas las variables
#!pip install dimod
Para la generación de variables con Dewava se utiliza mucho el formato de representación de Python de tipo f’xxxx{}i’, para el lector que no lo conozca a continuación se muestran una serie de ejemplos, que ayudan a comprender su uso.
i="casa"
f'aaaa_{i}'
'aaaa_casa'
# Otra forma es la siguiente
'aaa_{}'.format(i)
'aaa_casa'
A continuación implementado el modelo QUBO. Hay que observar que para definir las variables se crea un diccionario, de tal manera que los índices son los pares (i,j) que hacen referencia a la variable \(x_{ij}\).
from dimod import AdjVectorBQM
# AdjVectorBQMy AdjDictBQM ahora son alias para BinaryQuadraticModely DictBQM respectivamente
#en lugar de tener su propia implementación con una API ligeramente diferente
bqm = AdjVectorBQM('BINARY')
# Creamos el diccionario que contiene las variables
x = {(i, j): bqm.add_variable((f'x_{i}', j), 0) # Inicializamos con bias=0
for i in range(num_points)
for j in range(num_clusters)
}
x
{(0, 0): ('x_0', 0),
(0, 1): ('x_0', 1),
(0, 2): ('x_0', 2),
(1, 0): ('x_1', 0),
(1, 1): ('x_1', 1),
(1, 2): ('x_1', 2),
(2, 0): ('x_2', 0),
(2, 1): ('x_2', 1),
(2, 2): ('x_2', 2),
(3, 0): ('x_3', 0),
(3, 1): ('x_3', 1),
(3, 2): ('x_3', 2),
(4, 0): ('x_4', 0),
(4, 1): ('x_4', 1),
(4, 2): ('x_4', 2),
(5, 0): ('x_5', 0),
(5, 1): ('x_5', 1),
(5, 2): ('x_5', 2),
(6, 0): ('x_6', 0),
(6, 1): ('x_6', 1),
(6, 2): ('x_6', 2),
(7, 0): ('x_7', 0),
(7, 1): ('x_7', 1),
(7, 2): ('x_7', 2),
(8, 0): ('x_8', 0),
(8, 1): ('x_8', 1),
(8, 2): ('x_8', 2),
(9, 0): ('x_9', 0),
(9, 1): ('x_9', 1),
(9, 2): ('x_9', 2)}
x[(0,0]
Cell In[11], line 1
x[(0,0]
^
SyntaxError: closing parenthesis ']' does not match opening parenthesis '('
Realmente interesa ver el objeto de tipo BQM que hemos generado. Veámoslo con la siguiente instrucción:
bqm
Float64BQM({('x_0', 0): 0.0, ('x_0', 1): 0.0, ('x_0', 2): 0.0, ('x_1', 0): 0.0, ('x_1', 1): 0.0, ('x_1', 2): 0.0, ('x_2', 0): 0.0, ('x_2', 1): 0.0, ('x_2', 2): 0.0, ('x_3', 0): 0.0, ('x_3', 1): 0.0, ('x_3', 2): 0.0, ('x_4', 0): 0.0, ('x_4', 1): 0.0, ('x_4', 2): 0.0, ('x_5', 0): 0.0, ('x_5', 1): 0.0, ('x_5', 2): 0.0, ('x_6', 0): 0.0, ('x_6', 1): 0.0, ('x_6', 2): 0.0, ('x_7', 0): 0.0, ('x_7', 1): 0.0, ('x_7', 2): 0.0, ('x_8', 0): 0.0, ('x_8', 1): 0.0, ('x_8', 2): 0.0, ('x_9', 0): 0.0, ('x_9', 1): 0.0, ('x_9', 2): 0.0}, {}, 0.0, 'BINARY')
Las penalizaciones que imponemos van a ser proporcionales a la distancia que hay entre cada par de puntos
from itertools import combinations
for i, j in combinations(range(num_points), r=2):
for k in range(num_clusters):
bqm.add_interaction(x[i, k], x[j, k], distances[i, j])
distances[(0,1)]
0.14171301363998623
print(bqm)
Float64BQM({('x_0', 0): 0.0, ('x_0', 1): 0.0, ('x_0', 2): 0.0, ('x_1', 0): 0.0, ('x_1', 1): 0.0, ('x_1', 2): 0.0, ('x_2', 0): 0.0, ('x_2', 1): 0.0, ('x_2', 2): 0.0, ('x_3', 0): 0.0, ('x_3', 1): 0.0, ('x_3', 2): 0.0, ('x_4', 0): 0.0, ('x_4', 1): 0.0, ('x_4', 2): 0.0, ('x_5', 0): 0.0, ('x_5', 1): 0.0, ('x_5', 2): 0.0, ('x_6', 0): 0.0, ('x_6', 1): 0.0, ('x_6', 2): 0.0, ('x_7', 0): 0.0, ('x_7', 1): 0.0, ('x_7', 2): 0.0, ('x_8', 0): 0.0, ('x_8', 1): 0.0, ('x_8', 2): 0.0, ('x_9', 0): 0.0, ('x_9', 1): 0.0, ('x_9', 2): 0.0}, {(('x_1', 0), ('x_0', 0)): 0.14171301363998623, (('x_1', 1), ('x_0', 1)): 0.14171301363998623, (('x_1', 2), ('x_0', 2)): 0.14171301363998623, (('x_2', 0), ('x_0', 0)): 0.04786461576403033, (('x_2', 0), ('x_1', 0)): 0.13713890777482518, (('x_2', 1), ('x_0', 1)): 0.04786461576403033, (('x_2', 1), ('x_1', 1)): 0.13713890777482518, (('x_2', 2), ('x_0', 2)): 0.04786461576403033, (('x_2', 2), ('x_1', 2)): 0.13713890777482518, (('x_3', 0), ('x_0', 0)): 2.060083502578733, (('x_3', 0), ('x_1', 0)): 2.0982814520019986, (('x_3', 0), ('x_2', 0)): 2.1079322079296503, (('x_3', 1), ('x_0', 1)): 2.060083502578733, (('x_3', 1), ('x_1', 1)): 2.0982814520019986, (('x_3', 1), ('x_2', 1)): 2.1079322079296503, (('x_3', 2), ('x_0', 2)): 2.060083502578733, (('x_3', 2), ('x_1', 2)): 2.0982814520019986, (('x_3', 2), ('x_2', 2)): 2.1079322079296503, (('x_4', 0), ('x_0', 0)): 2.021445339881007, (('x_4', 0), ('x_1', 0)): 2.0466320647533833, (('x_4', 0), ('x_2', 0)): 2.0689638606906113, (('x_4', 0), ('x_3', 0)): 0.19892225900002158, (('x_4', 1), ('x_0', 1)): 2.021445339881007, (('x_4', 1), ('x_1', 1)): 2.0466320647533833, (('x_4', 1), ('x_2', 1)): 2.0689638606906113, (('x_4', 1), ('x_3', 1)): 0.19892225900002158, (('x_4', 2), ('x_0', 2)): 2.021445339881007, (('x_4', 2), ('x_1', 2)): 2.0466320647533833, (('x_4', 2), ('x_2', 2)): 2.0689638606906113, (('x_4', 2), ('x_3', 2)): 0.19892225900002158, (('x_5', 0), ('x_0', 0)): 1.988012861806546, (('x_5', 0), ('x_1', 0)): 2.0359878071872926, (('x_5', 0), ('x_2', 0)): 2.0358280560977313, (('x_5', 0), ('x_3', 0)): 0.16266181570569063, (('x_5', 0), ('x_4', 0)): 0.3375104609602114, (('x_5', 1), ('x_0', 1)): 1.988012861806546, (('x_5', 1), ('x_1', 1)): 2.0359878071872926, (('x_5', 1), ('x_2', 1)): 2.0358280560977313, (('x_5', 1), ('x_3', 1)): 0.16266181570569063, (('x_5', 1), ('x_4', 1)): 0.3375104609602114, (('x_5', 2), ('x_0', 2)): 1.988012861806546, (('x_5', 2), ('x_1', 2)): 2.0359878071872926, (('x_5', 2), ('x_2', 2)): 2.0358280560977313, (('x_5', 2), ('x_3', 2)): 0.16266181570569063, (('x_5', 2), ('x_4', 2)): 0.3375104609602114, (('x_6', 0), ('x_0', 0)): 2.2268504592580047, (('x_6', 0), ('x_1', 0)): 2.2509996278268907, (('x_6', 0), ('x_2', 0)): 2.2743432514648183, (('x_6', 0), ('x_3', 0)): 0.27133728939707086, (('x_6', 0), ('x_4', 0)): 0.205609041974235, (('x_6', 0), ('x_5', 0)): 0.43331279341820195, (('x_6', 1), ('x_0', 1)): 2.2268504592580047, (('x_6', 1), ('x_1', 1)): 2.2509996278268907, (('x_6', 1), ('x_2', 1)): 2.2743432514648183, (('x_6', 1), ('x_3', 1)): 0.27133728939707086, (('x_6', 1), ('x_4', 1)): 0.205609041974235, (('x_6', 1), ('x_5', 1)): 0.43331279341820195, (('x_6', 2), ('x_0', 2)): 2.2268504592580047, (('x_6', 2), ('x_1', 2)): 2.2509996278268907, (('x_6', 2), ('x_2', 2)): 2.2743432514648183, (('x_6', 2), ('x_3', 2)): 0.27133728939707086, (('x_6', 2), ('x_4', 2)): 0.205609041974235, (('x_6', 2), ('x_5', 2)): 0.43331279341820195, (('x_7', 0), ('x_0', 0)): 1.3786024797238556, (('x_7', 0), ('x_1', 0)): 1.5018548366862834, (('x_7', 0), ('x_2', 0)): 1.4135584280215412, (('x_7', 0), ('x_3', 0)): 1.4649749253207014, (('x_7', 0), ('x_4', 0)): 1.568275600203059, (('x_7', 0), ('x_5', 0)): 1.3129898372728241, (('x_7', 0), ('x_6', 0)): 1.7303872590573925, (('x_7', 1), ('x_0', 1)): 1.3786024797238556, (('x_7', 1), ('x_1', 1)): 1.5018548366862834, (('x_7', 1), ('x_2', 1)): 1.4135584280215412, (('x_7', 1), ('x_3', 1)): 1.4649749253207014, (('x_7', 1), ('x_4', 1)): 1.568275600203059, (('x_7', 1), ('x_5', 1)): 1.3129898372728241, (('x_7', 1), ('x_6', 1)): 1.7303872590573925, (('x_7', 2), ('x_0', 2)): 1.3786024797238556, (('x_7', 2), ('x_1', 2)): 1.5018548366862834, (('x_7', 2), ('x_2', 2)): 1.4135584280215412, (('x_7', 2), ('x_3', 2)): 1.4649749253207014, (('x_7', 2), ('x_4', 2)): 1.568275600203059, (('x_7', 2), ('x_5', 2)): 1.3129898372728241, (('x_7', 2), ('x_6', 2)): 1.7303872590573925, (('x_8', 0), ('x_0', 0)): 1.6479918054288936, (('x_8', 0), ('x_1', 0)): 1.7703292966235378, (('x_8', 0), ('x_2', 0)): 1.6831896457539017, (('x_8', 0), ('x_3', 0)): 1.4611456608927758, (('x_8', 0), ('x_4', 0)): 1.5928397182594412, (('x_8', 0), ('x_5', 0)): 1.3008016034427274, (('x_8', 0), ('x_6', 0)): 1.7322696120830763, (('x_8', 0), ('x_7', 0)): 0.2697634806026235, (('x_8', 1), ('x_0', 1)): 1.6479918054288936, (('x_8', 1), ('x_1', 1)): 1.7703292966235378, (('x_8', 1), ('x_2', 1)): 1.6831896457539017, (('x_8', 1), ('x_3', 1)): 1.4611456608927758, (('x_8', 1), ('x_4', 1)): 1.5928397182594412, (('x_8', 1), ('x_5', 1)): 1.3008016034427274, (('x_8', 1), ('x_6', 1)): 1.7322696120830763, (('x_8', 1), ('x_7', 1)): 0.2697634806026235, (('x_8', 2), ('x_0', 2)): 1.6479918054288936, (('x_8', 2), ('x_1', 2)): 1.7703292966235378, (('x_8', 2), ('x_2', 2)): 1.6831896457539017, (('x_8', 2), ('x_3', 2)): 1.4611456608927758, (('x_8', 2), ('x_4', 2)): 1.5928397182594412, (('x_8', 2), ('x_5', 2)): 1.3008016034427274, (('x_8', 2), ('x_6', 2)): 1.7322696120830763, (('x_8', 2), ('x_7', 2)): 0.2697634806026235, (('x_9', 0), ('x_0', 0)): 1.3184677820847432, (('x_9', 0), ('x_1', 0)): 1.4395531331129483, (('x_9', 0), ('x_2', 0)): 1.3544761237410892, (('x_9', 0), ('x_3', 0)): 1.4263139402858502, (('x_9', 0), ('x_4', 0)): 1.52254503816272, (('x_9', 0), ('x_5', 0)): 1.2772333969863539, (('x_9', 0), ('x_6', 0)): 1.6892553634688006, (('x_9', 0), ('x_7', 0)): 0.07454051523423368, (('x_9', 0), ('x_8', 0)): 0.33130121905248167, (('x_9', 1), ('x_0', 1)): 1.3184677820847432, (('x_9', 1), ('x_1', 1)): 1.4395531331129483, (('x_9', 1), ('x_2', 1)): 1.3544761237410892, (('x_9', 1), ('x_3', 1)): 1.4263139402858502, (('x_9', 1), ('x_4', 1)): 1.52254503816272, (('x_9', 1), ('x_5', 1)): 1.2772333969863539, (('x_9', 1), ('x_6', 1)): 1.6892553634688006, (('x_9', 1), ('x_7', 1)): 0.07454051523423368, (('x_9', 1), ('x_8', 1)): 0.33130121905248167, (('x_9', 2), ('x_0', 2)): 1.3184677820847432, (('x_9', 2), ('x_1', 2)): 1.4395531331129483, (('x_9', 2), ('x_2', 2)): 1.3544761237410892, (('x_9', 2), ('x_3', 2)): 1.4263139402858502, (('x_9', 2), ('x_4', 2)): 1.52254503816272, (('x_9', 2), ('x_5', 2)): 1.2772333969863539, (('x_9', 2), ('x_6', 2)): 1.6892553634688006, (('x_9', 2), ('x_7', 2)): 0.07454051523423368, (('x_9', 2), ('x_8', 2)): 0.33130121905248167}, 0.0, 'BINARY')
28.2. Restricción.#
Añadimos la restricción para conseguir que las variables sean discretas, para ello debemos conseguir que para cara puntoa (es decir para cada subíndice i) la suma en el suíndice j sea 1. de esta manera conseguimos que cada punto pertenezca a uno y solo uno de los clúster.
for i in range(num_points):
bqm.add_linear_equality_constraint(
[(x[i, k], 1.0) for k in range(num_clusters)],
constant=-1.0,
lagrange_multiplier=one_hot_penalty
)
28.3. Resolución.#
Utilizamos ahora el solver SimulatedAnnealingSampler,
from neal import SimulatedAnnealingSampler
response = SimulatedAnnealingSampler().sample(bqm, num_reads=100, num_sweeps=10000).truncate(3)
print(response)
('x_0', 0) ('x_0', 1) ('x_0', 2) ('x_1', 0) ... ('x_9', 2) energy num_oc.
0 0 0 1 0 ... 0 2.611675 1
1 0 0 1 0 ... 0 2.611675 1
2 0 0 1 0 ... 0 2.611675 1
['BINARY', 3 rows, 3 samples, 30 variables]
response.first.sample
{('x_0', 0): 0,
('x_0', 1): 0,
('x_0', 2): 1,
('x_1', 0): 0,
('x_1', 1): 0,
('x_1', 2): 1,
('x_2', 0): 0,
('x_2', 1): 0,
('x_2', 2): 1,
('x_3', 0): 1,
('x_3', 1): 0,
('x_3', 2): 0,
('x_4', 0): 1,
('x_4', 1): 0,
('x_4', 2): 0,
('x_5', 0): 1,
('x_5', 1): 0,
('x_5', 2): 0,
('x_6', 0): 1,
('x_6', 1): 0,
('x_6', 2): 0,
('x_7', 0): 0,
('x_7', 1): 1,
('x_7', 2): 0,
('x_8', 0): 0,
('x_8', 1): 1,
('x_8', 2): 0,
('x_9', 0): 0,
('x_9', 1): 1,
('x_9', 2): 0}
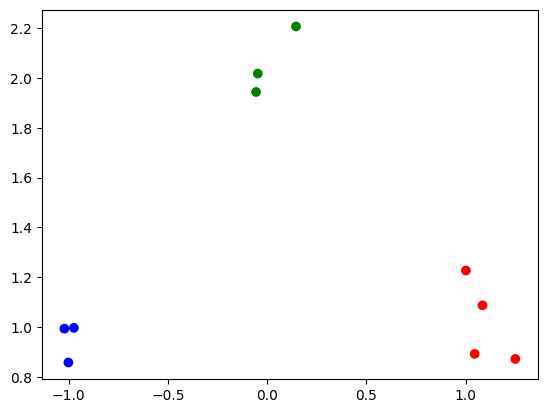
best_solution = response.first.sample
assignments = {point: cluster for (point, cluster), value in best_solution.items() if value}
print(assignments)
{'x_0': 2, 'x_1': 2, 'x_2': 2, 'x_3': 0, 'x_4': 0, 'x_5': 0, 'x_6': 0, 'x_7': 1, 'x_8': 1, 'x_9': 1}
colors = ['r', 'g', 'b']
point_colors = [colors[assignments['x_{}'.format(i)]] for i in range(len(points))]
plt.scatter(*zip(*points), c=point_colors)
<matplotlib.collections.PathCollection at 0x18ff54337c0>
28.4. Otro ejemplo.#
Ahora hacemos lo mismo que antes, pero con otro conjunto de datos
import numpy as np
origenes = np.array([[1,1],[6,6]])
puntos = np.array([[11,10],[2,1],[1.5,2],[3,2],[0,1],[0.5,1],[7,6],[8,7],[5,6],[8,7],[6,8],[7,7],[2,2],[11,11]])
distances = {(i, j): np.sqrt(np.sum(np.square(puntos[i] - puntos[j])))+
np.sqrt(np.sum(((puntos[1]+puntos[2])/2)-origenes[0]))
for i in range(len(puntos))
for j in range(len(puntos))
if i != j
}
np.sqrt(np.sum(((puntos[1]+puntos[2])/2)-origenes[0]))
1.118033988749895
#distances
from dimod import AdjVectorBQM
bqm = AdjVectorBQM('BINARY')
num_clusters = 2
x = {(i, j): bqm.add_variable((f'x_{i}', j), 0)
for i in range(len(puntos))
for j in range(num_clusters)
}
from itertools import combinations
for i, j in combinations(range(len(puntos)), r=2):
for k in range(num_clusters):
bqm.add_interaction(x[i, k], x[j, k], distances[i, j])
one_hot_penalty = 100
for i in range(len(puntos)):
bqm.add_linear_equality_constraint(
[(x[i, k], 1.0) for k in range(num_clusters)],
constant=-1.0,
lagrange_multiplier=one_hot_penalty
)
bqm.add_linear_equality_constraint(
[(x[i, 0], 1.0) for i in range(len(puntos))],
constant=-int(len(puntos)/2),
lagrange_multiplier=one_hot_penalty
)
from neal import SimulatedAnnealingSampler
response = SimulatedAnnealingSampler().sample(bqm, num_reads=100, num_sweeps=10000).truncate(3)
print(response)
('x_0', 0) ('x_0', 1) ('x_1', 0) ('x_1', 1) ... ('x_9', 1) energy num_oc.
0 1 0 0 1 ... 0 172.385484 1
1 1 0 0 1 ... 0 172.385484 1
2 1 0 0 1 ... 0 172.385484 1
['BINARY', 3 rows, 3 samples, 28 variables]
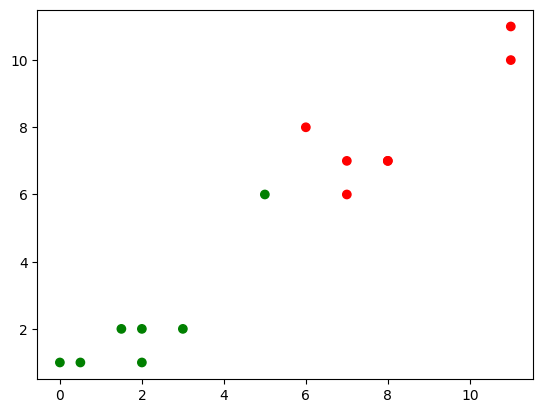
best_solution = response.first.sample
assignments = {point: cluster for (point, cluster), value in best_solution.items() if value}
print(assignments)
{'x_0': 0, 'x_1': 1, 'x_10': 0, 'x_11': 0, 'x_12': 1, 'x_13': 0, 'x_2': 1, 'x_3': 1, 'x_4': 1, 'x_5': 1, 'x_6': 0, 'x_7': 0, 'x_8': 1, 'x_9': 0}
import matplotlib.pyplot as plt
colors = ['r', 'g', 'b']
point_colors = [colors[assignments['x_{}'.format(i)]] for i in range(len(puntos))]
plt.scatter(*zip(*puntos), c=point_colors)
<matplotlib.collections.PathCollection at 0x18ff5480280>
28.5. Otra prueba#
origenes = np.array([[1,1],[6,6]])
puntos = np.array([[1,0],[2,1],[1.5,2],[3,2],[0,1],[0.5,1],[7,6],[8,7],[5,6],[8,7],[6,8],[7,7]])
distances = {(i, j): np.sqrt(np.sum(np.square(puntos[i] - puntos[j])))
for i in range(len(puntos))
for j in range(len(puntos))
if i != j
}
one_hot_penalty = 10
#distances
from dimod import AdjVectorBQM
num_clusters = 2
bqm = AdjVectorBQM('BINARY')
x = {(i, j): bqm.add_variable((f'x_{i}', j), 0)
for i in range(len(puntos))
#for j in range(num_clusters-1)
for j in range(num_clusters)
}
#x
from itertools import combinations
for i, j in combinations(range(num_points), r=2):
for k in range(num_clusters):
bqm.add_interaction(x[i, k], x[j, k], distances[i, j])
from itertools import combinations
print(bqm)
AdjVectorBQM({('x_0', 0): 0.0, ('x_0', 1): 0.0, ('x_1', 0): 0.0, ('x_1', 1): 0.0, ('x_2', 0): 0.0, ('x_2', 1): 0.0, ('x_3', 0): 0.0, ('x_3', 1): 0.0, ('x_4', 0): 0.0, ('x_4', 1): 0.0, ('x_5', 0): 0.0, ('x_5', 1): 0.0, ('x_6', 0): 0.0, ('x_6', 1): 0.0, ('x_7', 0): 0.0, ('x_7', 1): 0.0, ('x_8', 0): 0.0, ('x_8', 1): 0.0, ('x_9', 0): 0.0, ('x_9', 1): 0.0, ('x_10', 0): 0.0, ('x_10', 1): 0.0, ('x_11', 0): 0.0, ('x_11', 1): 0.0}, {(('x_0', 0), ('x_1', 0)): 1.4142135623730951, (('x_0', 0), ('x_2', 0)): 2.0615528128088303, (('x_0', 0), ('x_3', 0)): 2.8284271247461903, (('x_0', 0), ('x_4', 0)): 1.4142135623730951, (('x_0', 0), ('x_5', 0)): 1.118033988749895, (('x_0', 0), ('x_6', 0)): 8.48528137423857, (('x_0', 0), ('x_7', 0)): 9.899494936611665, (('x_0', 0), ('x_8', 0)): 7.211102550927978, (('x_0', 1), ('x_1', 1)): 1.4142135623730951, (('x_0', 1), ('x_2', 1)): 2.0615528128088303, (('x_0', 1), ('x_3', 1)): 2.8284271247461903, (('x_0', 1), ('x_4', 1)): 1.4142135623730951, (('x_0', 1), ('x_5', 1)): 1.118033988749895, (('x_0', 1), ('x_6', 1)): 8.48528137423857, (('x_0', 1), ('x_7', 1)): 9.899494936611665, (('x_0', 1), ('x_8', 1)): 7.211102550927978, (('x_1', 0), ('x_2', 0)): 1.118033988749895, (('x_1', 0), ('x_3', 0)): 1.4142135623730951, (('x_1', 0), ('x_4', 0)): 2.0, (('x_1', 0), ('x_5', 0)): 1.5, (('x_1', 0), ('x_6', 0)): 7.0710678118654755, (('x_1', 0), ('x_7', 0)): 8.48528137423857, (('x_1', 0), ('x_8', 0)): 5.830951894845301, (('x_1', 1), ('x_2', 1)): 1.118033988749895, (('x_1', 1), ('x_3', 1)): 1.4142135623730951, (('x_1', 1), ('x_4', 1)): 2.0, (('x_1', 1), ('x_5', 1)): 1.5, (('x_1', 1), ('x_6', 1)): 7.0710678118654755, (('x_1', 1), ('x_7', 1)): 8.48528137423857, (('x_1', 1), ('x_8', 1)): 5.830951894845301, (('x_2', 0), ('x_3', 0)): 1.5, (('x_2', 0), ('x_4', 0)): 1.8027756377319946, (('x_2', 0), ('x_5', 0)): 1.4142135623730951, (('x_2', 0), ('x_6', 0)): 6.800735254367722, (('x_2', 0), ('x_7', 0)): 8.200609733428363, (('x_2', 0), ('x_8', 0)): 5.315072906367325, (('x_2', 1), ('x_3', 1)): 1.5, (('x_2', 1), ('x_4', 1)): 1.8027756377319946, (('x_2', 1), ('x_5', 1)): 1.4142135623730951, (('x_2', 1), ('x_6', 1)): 6.800735254367722, (('x_2', 1), ('x_7', 1)): 8.200609733428363, (('x_2', 1), ('x_8', 1)): 5.315072906367325, (('x_3', 0), ('x_4', 0)): 3.1622776601683795, (('x_3', 0), ('x_5', 0)): 2.692582403567252, (('x_3', 0), ('x_6', 0)): 5.656854249492381, (('x_3', 0), ('x_7', 0)): 7.0710678118654755, (('x_3', 0), ('x_8', 0)): 4.47213595499958, (('x_3', 1), ('x_4', 1)): 3.1622776601683795, (('x_3', 1), ('x_5', 1)): 2.692582403567252, (('x_3', 1), ('x_6', 1)): 5.656854249492381, (('x_3', 1), ('x_7', 1)): 7.0710678118654755, (('x_3', 1), ('x_8', 1)): 4.47213595499958, (('x_4', 0), ('x_5', 0)): 0.5, (('x_4', 0), ('x_6', 0)): 8.602325267042627, (('x_4', 0), ('x_7', 0)): 10.0, (('x_4', 0), ('x_8', 0)): 7.0710678118654755, (('x_4', 1), ('x_5', 1)): 0.5, (('x_4', 1), ('x_6', 1)): 8.602325267042627, (('x_4', 1), ('x_7', 1)): 10.0, (('x_4', 1), ('x_8', 1)): 7.0710678118654755, (('x_5', 0), ('x_6', 0)): 8.200609733428363, (('x_5', 0), ('x_7', 0)): 9.604686356149273, (('x_5', 0), ('x_8', 0)): 6.726812023536855, (('x_5', 1), ('x_6', 1)): 8.200609733428363, (('x_5', 1), ('x_7', 1)): 9.604686356149273, (('x_5', 1), ('x_8', 1)): 6.726812023536855, (('x_6', 0), ('x_7', 0)): 1.4142135623730951, (('x_6', 0), ('x_8', 0)): 2.0, (('x_6', 1), ('x_7', 1)): 1.4142135623730951, (('x_6', 1), ('x_8', 1)): 2.0, (('x_7', 0), ('x_8', 0)): 3.1622776601683795, (('x_7', 1), ('x_8', 1)): 3.1622776601683795}, 0.0, 'BINARY')
one_hot_penalty = 28
for i in range(len(puntos)):
bqm.add_linear_equality_constraint(
[(x[i, k], 1.0) for k in range(num_clusters)],
constant=-1.0,
lagrange_multiplier=one_hot_penalty
)
#for i in range(len(puntos)):
bqm.add_linear_equality_constraint(
[(x[i, 1], 1.0) for i in range(len(puntos))],
constant=-int(len(puntos)/2),
lagrange_multiplier=one_hot_penalty
)
from neal import SimulatedAnnealingSampler
response = SimulatedAnnealingSampler().sample(bqm, num_reads=100, num_sweeps=10000).truncate(3)
print(response)
('x_0', 0) ('x_0', 1) ('x_1', 0) ('x_1', 1) ... ('x_9', 1) energy num_oc.
0 1 0 1 0 ... 1 32.517029 1
1 1 0 1 0 ... 1 32.517029 1
2 1 0 1 0 ... 1 32.517029 1
['BINARY', 3 rows, 3 samples, 24 variables]
best_solution = response.first.sample
assignments = {point: cluster for (point, cluster), value in best_solution.items() if value}
print(assignments)
{'x_0': 0, 'x_1': 0, 'x_10': 1, 'x_11': 1, 'x_2': 0, 'x_3': 0, 'x_4': 0, 'x_5': 0, 'x_6': 1, 'x_7': 1, 'x_8': 1, 'x_9': 1}
best_solution
{('x_0', 0): 1,
('x_0', 1): 0,
('x_1', 0): 1,
('x_1', 1): 0,
('x_10', 0): 0,
('x_10', 1): 1,
('x_11', 0): 0,
('x_11', 1): 1,
('x_2', 0): 1,
('x_2', 1): 0,
('x_3', 0): 1,
('x_3', 1): 0,
('x_4', 0): 1,
('x_4', 1): 0,
('x_5', 0): 1,
('x_5', 1): 0,
('x_6', 0): 0,
('x_6', 1): 1,
('x_7', 0): 0,
('x_7', 1): 1,
('x_8', 0): 0,
('x_8', 1): 1,
('x_9', 0): 0,
('x_9', 1): 1}
###Con DQM
Vamos a cambiar un poco el ejemplo anterior, y vamos a suponer que tenemos dos coches ubicados en un lugar definido por unas coordenadas. Después tenemos otros coches en otros puntos, también definidos por un par de coordenadas.
A cada coche le vamos a dar una preferencia de asignación a un coche u otro. Esta preferencia está dada por un par de valores, cada valor del par indica la preferencia por un coche u otro. Un valor más pequeño indica mayor preferencia (esto es debido a que al fina la ecuación que tratamos es de minimización).
Formulamos todo esto de la siguiente manera
from dimod import DiscreteQuadraticModel
from dwave.system import LeapHybridDQMSampler
sampler = LeapHybridDQMSampler()
origenes = np.array([[1,1],[6,6]]) # Los orígenes de los coches
puntos = np.array([[6.5,10],[2,1],[1.5,2],[3,2],[0,1],[0.5,1],[7,6],[8,7],[5,6],[8,7],[6,8],[7,7]])
Al final veo que lo de la celda anterior no lo utilizo para este caso, pero sí sería necesario cuando se calculen de forma programática las preferencias de cada punto. Las preferencias para este ejemplo lo asigno de forma manual en la siguiente celda, utilizo como criterio la cercanía de un punto a cada uno de los coches.
preferences = { "y_1": [2,1],
"y_2":[1,2],
"y_3" :[1,2],
"y_4": [1,2],
"y_5": [1,2],
"y_6" : [1,2],
"y_7":[2,1],
"y_8":[2,1],
"y_9":[2,1],
"y_10":[2,1],
"y_11":[2,1],
"y_12":[2,1]
}
num_coches = 2
dqm = DiscreteQuadraticModel()
Para ver la propiedad add_variable ver este enlace:
#Creamos las variables del modelo
for name in preferences:
dqm.add_variable(num_coches, label=name)
#Sacamos el número de variables
print(dqm.num_variables() )
12
for name in preferences:
dqm.set_linear(name, preferences[name])
Resolvemos el problema
sampleset = sampler.sample_dqm(dqm, label='Training - Asignacion puntos')
sampleset
SampleSet(rec.array([([0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1], 0., 1),
([0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1], 0., 1),
([1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1], 0., 1),
([1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1], 0., 1),
([1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0], 0., 1),
([1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0], 0., 1),
([1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1], 0., 1),
([0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1], 0., 1),
([0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1], 0., 1),
([1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0], 0., 1),
([1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0], 0., 1),
([0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0], 0., 1),
([0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0], 0., 1),
([0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0], 0., 1),
([1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1], 0., 1),
([0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1], 0., 1),
([1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1], 0., 1),
([0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0], 0., 1),
([0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1], 0., 1),
([0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1], 0., 1),
([1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1], 0., 1),
([1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1], 0., 1),
([1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1], 0., 1),
([1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0], 0., 1),
([0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1], 0., 1),
([1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1], 0., 1),
([1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1], 0., 1),
([0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1], 0., 1),
([1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0], 0., 1),
([1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0], 0., 1),
([0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1], 0., 1),
([0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0], 0., 1),
([1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1], 0., 1),
([1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1], 0., 1),
([0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1], 0., 1),
([0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0], 0., 1),
([0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1], 0., 1),
([0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1], 0., 1),
([1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0], 0., 1),
([1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1], 0., 1),
([0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0], 0., 1),
([1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1], 0., 1),
([1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1], 0., 1),
([0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0], 0., 1),
([0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1], 0., 1),
([0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1], 0., 1),
([1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0], 0., 1),
([1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1], 0., 1),
([0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0], 0., 1),
([1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0], 0., 1),
([0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0], 0., 1),
([0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1], 0., 1),
([0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1], 0., 1),
([1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1], 0., 1),
([1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1], 0., 1),
([1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0], 0., 1),
([0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0], 0., 1),
([1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1], 0., 1),
([0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1], 0., 1),
([1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0], 0., 1),
([0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1], 0., 1),
([0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0], 0., 1),
([0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0], 0., 1),
([1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1], 0., 1),
([1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0], 0., 1),
([0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0], 0., 1),
([0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0], 0., 1),
([1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1], 0., 1),
([0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0], 0., 1),
([1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1], 0., 1),
([1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1], 0., 1),
([0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1], 0., 1),
([1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1], 0., 1),
([0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1], 0., 1),
([1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0], 0., 1),
([0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1], 0., 1),
([1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0], 0., 1),
([1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1], 0., 1),
([0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1], 0., 1),
([0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1], 0., 1),
([1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0], 0., 1),
([0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0], 0., 1),
([0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1], 0., 1),
([0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0], 0., 1),
([0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0], 0., 1),
([1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0], 0., 1),
([1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1], 0., 1),
([1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0], 0., 1)],
dtype=[('sample', '<i4', (12,)), ('energy', '<f8'), ('num_occurrences', '<i8')]), Variables(['y_1', 'y_2', 'y_3', 'y_4', 'y_5', 'y_6', 'y_7', 'y_8', 'y_9', 'y_10', 'y_11', 'y_12']), {'qpu_access_time': 31804, 'charge_time': 5000000, 'run_time': 5117988, 'problem_id': 'ce947f3a-9dba-422e-a429-34de48de0d37', 'problem_label': 'Training - Asignacion puntos'}, 'INTEGER')
sample = sampleset.first.sample
shift_schedule=[ [] for i in range(num_coches)]
for key, val in sample.items():
shift_schedule[val].append(key)
shift_schedule
[['y_1', 'y_2', 'y_3', 'y_9', 'y_10'],
['y_4', 'y_5', 'y_6', 'y_7', 'y_8', 'y_11', 'y_12']]
sample.items()
dict_items([('y_1', 0), ('y_2', 0), ('y_3', 0), ('y_4', 1), ('y_5', 1), ('y_6', 1), ('y_7', 1), ('y_8', 1), ('y_9', 0), ('y_10', 0), ('y_11', 1), ('y_12', 1)])
28.6. Otra forma con DQM.#
En esta ocasión voy a utilizar la información que me dan las distancias a cada centro de salida
import numpy as np
origenes = np.array([[1,1],[6,6]])
puntos = np.array([[6.5,10],[2,1],[1.5,2],[3,2],[0,1],[0.5,1],[7,6],[8,7],[5,6],[8,7],[6,8],[7,7]])
distances = {(i, j): np.sqrt(np.sum(np.square(puntos[i] - origenes[j])))
for i in range(len(puntos))
for j in range(len(origenes))
#if i != j
}
n_coches = len(origenes)
from dimod import DiscreteQuadraticModel
from dwave.system import LeapHybridDQMSampler
dqm=DiscreteQuadraticModel()
for punto in range(len(puntos)):
dqm.add_variable(n_coches,label=punto)
# Cosntruimos la función objetivo
for punto in range(len(puntos)):
#for coche in range(len(origenes)):
dqm.set_linear_case(punto,0,distances[punto,0])
gamma = 20
for i in range(len(puntos)):
dqm.set_linear_case(i,0,gamma)
dqm.set_linear_case(i,1,gamma)
for j in range(i+1, len(puntos)):
dqm.set_quadratic_case(i,0,j,0,2*gamma)
dqm.set_quadratic_case(i,1,j,1,2*gamma)
dqm.set_quadratic_case(i,0,j,1,-2*gamma)
dqm.set_quadratic_case(i,1,j,0,-2*gamma)
sampler = LeapHybridDQMSampler()
sampleset = sampler.sample_dqm(dqm, label='distribucion puntos coche')
sample = sampleset.first.sample
sample
{0: 0, 1: 0, 2: 1, 3: 1, 4: 0, 5: 0, 6: 0, 7: 1, 8: 1, 9: 1, 10: 1, 11: 0}
distances
sampleset
SampleSet(rec.array([([1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0], 0., 1),
([1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0], 0., 1),
([1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0], 0., 1),
([0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0], 0., 1),
([1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0], 0., 1),
([1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0], 0., 1),
([0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1], 0., 1),
([0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0], 0., 1),
([1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0], 0., 1),
([0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1], 0., 1),
([1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1], 0., 1),
([1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0], 0., 1),
([0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0], 320., 1),
([0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0], 0., 1),
([0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0], 80., 1),
([1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0], 0., 1),
([0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1], 80., 1),
([1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0], 0., 1),
([0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0], 0., 1),
([1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1], 320., 1),
([0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1], 80., 1),
([1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0], 80., 1),
([0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0], 80., 1),
([1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1], 80., 1)],
dtype=[('sample', '<i4', (12,)), ('energy', '<f8'), ('num_occurrences', '<i8')]), Variables(range(0, 12)), {'qpu_access_time': 58469, 'charge_time': 5000000, 'run_time': 5053213, 'problem_id': '410aa80e-5a8f-4497-95c7-efd83f30e2b0', 'problem_label': 'distribucion puntos coche'}, 'INTEGER')