18. Partición de un gráfo con DQM#
El objetivo de este ejercicio es conseguir una partición de un grafo, de tal manera que los subconjuntos obtenidos tengan el mismo número de nodos y las conexiones entre los subgrupos sean las menos posibles. Es un ejercico similar al que se ve en este enlace, pero en este caso utilizando DQM.
Comenzamos cargando los módulos que vamos a necesitar
from dimod import DiscreteQuadraticModel, ExactDQMSolver
from itertools import combinations
import networkx as nx
18.1. Partción del grafo en más de dos subconjuntos.#
Creamos el grafo con el que vamos a trabajar
edges = [
(1, 2), (2, 3), (1, 3),
(4, 5), (5, 6), (4, 6),
(7, 8), (8, 9), (7, 9),
(2, 4), (4, 8)
]
nodes = sorted(set().union(*edges))
graph = nx.Graph(edges)
nx.draw(graph, with_labels=True)
18.2. Variables de decisión#
Para este jercicio, asignamos variables \(x_{i,k} por cada noro \)i\( y conjunto de vértices \)k\(. Toma el valor 1 si el nodo \)i\( está en el conjunto \)k$.
Creamos las variable discretas de la siguiente manera
dqm = DiscreteQuadraticModel()
m = 3
n = len(nodes)
for node in nodes:
dqm.add_variable(m, node)
18.3. Objectivo#
En lugar de penalizar dos nodos que no son del mismo conjunto, recompensamos si
dos nodos pertenecen al mismo conjunto y
los dos nodos están conectados
\[\sum_a\sum_b -x_{a.k}x_{b,k}~~~\forall k\]
for a, b in edges:
for k in range(m):
dqm.set_quadratic_case(a, k, b, k, -1)
18.4. Restricciones#
El tamaño de cada conjunto debe ser igual a n/m
n es el núemro de nodos
m es el número de conjuntos que queremos tener
for k in range(m):
dqm.add_linear_equality_constraint(
[(i, k, 1.0) for i in nodes],
constant=-n/m,
lagrange_multiplier=10
)
Cada nodo sólo puede pertenecer a un conjunto. Esto lo gestionan de forma natural el objeto DQM y todos los solucionadores DQM.
res = ExactDQMSolver().sample_dqm(dqm).truncate(10)
print(res)
1 2 3 4 5 6 7 8 9 energy num_oc.
0 2 2 2 0 0 0 1 1 1 -9.0 1
1 2 2 2 1 1 1 0 0 0 -9.0 1
2 1 1 1 0 0 0 2 2 2 -9.0 1
3 0 0 0 1 1 1 2 2 2 -9.0 1
4 0 0 0 2 2 2 1 1 1 -9.0 1
5 1 1 1 2 2 2 0 0 0 -9.0 1
6 2 2 2 0 1 1 1 0 0 -6.0 1
7 0 0 0 1 2 2 2 1 1 -6.0 1
8 0 0 0 1 1 2 2 1 2 -6.0 1
9 0 1 1 1 0 0 2 2 2 -6.0 1
['INTEGER', 10 rows, 10 samples, 9 variables]
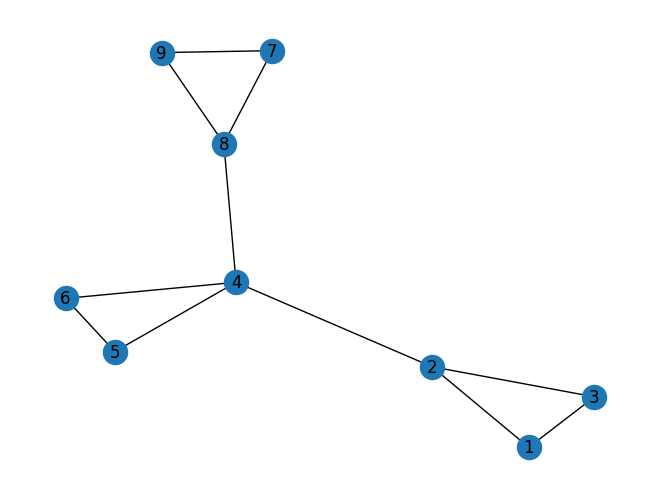
sample = res.first.sample
sample
{1: 2, 2: 2, 3: 2, 4: 0, 5: 0, 6: 0, 7: 1, 8: 1, 9: 1}
colors = ['r', 'g', 'b']
node_color = [colors[res.first.sample[node]] for node in nodes]
nx.draw(graph, with_labels=True, node_color=node_color, font_color='w')
También se puede resolver utilizando LeapHybridDQMSampler
from dwave.system import LeapHybridDQMSampler
sampler = LeapHybridDQMSampler()
res = sampler.sample_dqm(dqm, time_limit=None)
print(res)
1 2 3 4 5 6 7 8 9 energy num_oc.
0 2 2 2 0 0 0 1 1 1 -9.0 1
1 2 2 2 0 0 0 1 1 1 -9.0 1
2 1 1 1 0 0 0 2 2 2 -9.0 1
3 1 1 1 0 0 0 2 2 2 -9.0 1
4 2 2 2 1 1 1 0 0 0 -9.0 1
5 1 1 1 0 0 0 2 2 2 -9.0 1
6 2 2 2 1 1 1 0 0 0 -9.0 1
7 0 0 0 1 1 1 2 2 2 -9.0 1
8 1 1 1 0 0 0 2 2 2 -9.0 1
9 2 2 2 0 0 0 1 1 1 -9.0 1
10 2 2 2 0 0 0 1 1 1 -9.0 1
11 0 0 0 2 2 2 1 1 1 -9.0 1
12 2 2 2 0 0 0 1 1 1 -9.0 1
13 2 2 2 1 1 1 0 0 0 -9.0 1
14 2 2 2 1 1 1 0 0 0 -9.0 1
15 2 2 2 1 1 1 0 0 0 -9.0 1
16 0 0 0 2 2 2 1 1 1 -9.0 1
17 0 0 0 1 1 1 2 2 2 -9.0 1
18 0 0 0 1 1 1 2 2 2 -9.0 1
19 1 1 1 0 0 0 2 2 2 -9.0 1
21 1 1 1 0 0 0 2 2 2 -9.0 1
22 0 0 0 2 2 2 1 1 1 -9.0 1
23 0 0 0 1 1 1 2 2 2 -9.0 1
24 0 0 0 2 2 2 1 1 1 -9.0 1
25 1 1 1 0 0 0 2 2 2 -9.0 1
26 1 1 1 0 0 0 2 2 2 -9.0 1
27 0 0 0 2 2 2 1 1 1 -9.0 1
28 0 0 0 1 1 1 2 2 2 -9.0 1
29 0 0 0 1 1 1 2 2 2 -9.0 1
30 1 1 1 2 2 2 0 0 0 -9.0 1
31 0 0 0 1 1 1 2 2 2 -9.0 1
32 1 1 1 0 0 0 2 2 2 -9.0 1
33 1 1 1 2 2 2 0 0 0 -9.0 1
34 1 1 1 2 2 2 0 0 0 -9.0 1
35 1 1 1 2 2 2 0 0 0 -9.0 1
36 1 1 1 2 2 2 0 0 0 -9.0 1
37 0 0 0 1 1 1 2 2 2 -9.0 1
38 0 0 0 1 1 1 2 2 2 -9.0 1
39 0 0 0 1 1 1 2 2 2 -9.0 1
40 0 0 0 1 1 1 2 2 2 -9.0 1
41 1 1 1 2 2 2 0 0 0 -9.0 1
42 1 1 1 2 2 2 0 0 0 -9.0 1
43 2 2 2 1 1 1 0 0 0 -9.0 1
44 0 0 0 1 1 1 2 2 2 -9.0 1
45 2 2 2 1 1 1 0 0 0 -9.0 1
46 2 2 2 1 1 1 0 0 0 -9.0 1
47 0 0 0 2 2 2 1 1 1 -9.0 1
48 0 0 0 2 2 2 1 1 1 -9.0 1
49 1 1 1 2 2 2 0 0 0 -9.0 1
50 0 0 0 2 2 2 1 1 1 -9.0 1
51 1 1 1 0 0 0 2 2 2 -9.0 1
52 2 2 2 0 0 0 1 1 1 -9.0 1
53 0 0 0 2 2 2 1 1 1 -9.0 1
54 1 1 1 0 0 0 2 2 2 -9.0 1
55 2 2 2 0 0 0 1 1 1 -9.0 1
20 1 1 1 0 2 0 2 0 2 -6.0 1
56 2 1 2 1 2 1 0 0 0 -6.0 1
57 2 2 2 0 1 1 0 0 1 -6.0 1
58 1 2 2 2 1 1 0 0 0 -6.0 1
59 0 0 0 2 1 2 1 2 1 -6.0 1
60 1 2 2 2 1 1 0 0 0 -6.0 1
61 0 0 0 2 2 1 1 2 1 -6.0 1
62 1 2 1 2 1 2 0 0 0 -6.0 1
63 2 0 2 1 1 1 2 0 0 -5.0 1
64 1 1 1 2 2 0 2 0 0 -5.0 1
65 0 0 0 2 1 1 2 1 2 -5.0 1
66 2 1 2 1 1 0 0 0 2 -4.0 1
67 1 1 2 1 0 0 2 0 2 -4.0 1
68 1 1 2 0 2 2 0 0 1 -4.0 1
69 2 2 0 2 1 1 0 0 1 -4.0 1
70 0 1 0 1 2 1 0 2 2 -4.0 1
71 0 2 0 2 1 2 1 1 0 -4.0 1
72 1 2 1 1 0 0 2 0 2 -3.0 1
73 0 0 2 2 1 2 1 1 0 -3.0 1
74 1 2 2 0 2 0 0 1 1 -3.0 1
75 2 2 0 1 0 1 0 1 2 -3.0 1
76 0 2 2 2 1 0 1 0 1 -3.0 1
77 0 0 2 1 0 2 2 1 1 -3.0 1
78 1 0 0 2 2 1 0 2 1 -3.0 1
79 1 2 2 0 1 0 1 0 2 -3.0 1
80 0 1 0 1 2 2 1 2 0 -3.0 1
81 2 1 1 0 0 2 2 1 0 -2.0 1
82 1 2 1 0 2 1 0 2 0 -2.0 1
83 1 2 0 1 1 2 0 2 0 -2.0 1
84 1 2 0 1 1 0 0 2 2 -2.0 1
85 0 1 2 0 2 0 2 1 1 -2.0 1
86 0 2 0 0 1 2 1 2 1 -2.0 1
87 1 2 0 1 1 2 0 0 2 -2.0 1
['INTEGER', 88 rows, 88 samples, 9 variables]
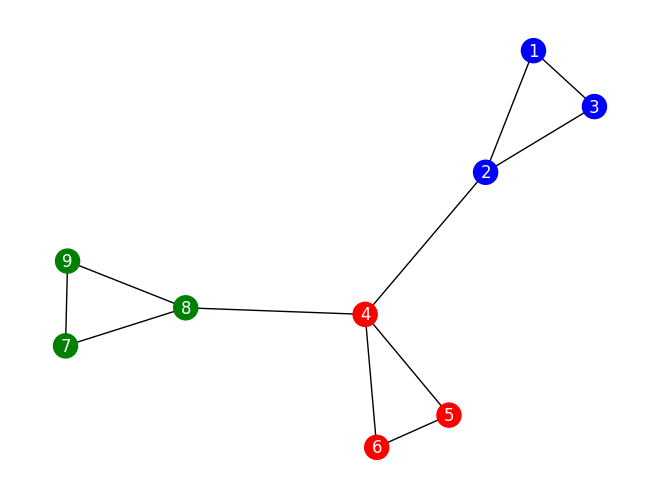
colors = ['r', 'g', 'b']
node_color = [colors[res.first.sample[node]] for node in nodes]
nx.draw(graph, with_labels=True, node_color=node_color, font_color='w')