Clasificación Logit

08 Sep 2018

Autor: Francisco Rodríguez

Contenido

Introducción
Construcción del modelo
Matriz de confusión
Librerías de R
Curva de ROC

Introducción

En post anteriores, ya se ha presentado el modelo de regresión logística, y se ha mostrado alguna de sus aplicaciones, cómo se interpretan los parámetros obtenidos en la regresión, así como la probabilidad de pertenecer a cada una de las categorías de la variables independiente. En este post se va a hacer una presentación de cómo utilizar este tipo de regresión para realizar un trabajo muy utilizado en machine learning como es el tema de la clasificación, es decir conocidas ciertas características de un individuo, en qué clase lo clasifico con mayores posibilidades de acertar.

Para presentar este método, se va a utilizar uno conjunto de datos similares a los ya empleados en un post anterior, me estoy refiriendo al fichero “DatosVasculopatia.csv” que contiene dos variables, una que será la variable dependiente que es de tipo dicotómico ( con sólo dos posibles valores 1 ó 0), y la otra contiene el denominado “índice tobillo brazo (ITB)” que es de tipo continuo. Comenzamos como siempre leyendo los datos.

datos<- read.csv("F:/MisCodigos/web/data/DatosVasculopatia2.csv",header = T,sep = "\t")
head(datos)

##       X Y
## 1 -3.83 0
## 2 -2.85 0
## 3 -6.23 0
## 4  8.57 1
## 5 -8.14 0
## 6 -4.93 0

Construcción del modelo

A continuación se procede a generar el modelo logístico con los datos mostrados anteriormente.

modelo<-glm(Y~X,family = binomial(link = "logit"), data = datos)
(summodelo<-summary(modelo))

## 
## Call:
## glm(formula = Y ~ X, family = binomial(link = "logit"), data = datos)
## 
## Deviance Residuals: 
##      Min        1Q    Median        3Q       Max  
## -2.42586  -0.08906   0.00730   0.11245   2.71905  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  0.09526    0.14684   0.649    0.516    
## X            1.07010    0.08567  12.491   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 1385.62  on 999  degrees of freedom
## Residual deviance:  306.23  on 998  degrees of freedom
## AIC: 310.23
## 
## Number of Fisher Scoring iterations: 8

Ahora al fichero original añadimos una columna con las probabilidades predichas.

datos$Prob<-modelo$fitted.values
head(datos)

##       X Y         Prob
## 1 -3.83 0 0.0179295281
## 2 -2.85 0 0.0495234490
## 3 -6.23 0 0.0013978077
## 4  8.57 1 0.9999054240
## 5 -8.14 0 0.0001812703
## 6 -4.93 0 0.0055947128

print("Número total de observaciones:")

## [1] "Número total de observaciones:"

nrow(datos)

## [1] 1000

Ahora ordenamos los datos por la variable X

orden<-order(datos$X,decreasing = TRUE)
head(datos[orden,])

##         X Y      Prob
## 175 10.00 1 0.9999795
## 740  9.99 1 0.9999793
## 14   9.98 1 0.9999791
## 496  9.97 1 0.9999789
## 8    9.92 1 0.9999777
## 458  9.92 1 0.9999777

tail(datos[orden,])

##         X Y         Prob
## 253 -9.88 0 2.816754e-05
## 304 -9.93 0 2.670008e-05
## 469 -9.95 0 2.613473e-05
## 119 -9.97 0 2.558136e-05
## 135 -9.98 0 2.530908e-05
## 540 -9.98 0 2.530908e-05

Como se puede ver en los dos bloques anteriores, una probabilidad alta está asociada a los valores de Y=1 y una probabilidad baja a los valores de Y=0. A la hora de hacer una clasificación con este método, el problema se plantea en el valor de corte de la probabilidad. El método más simple es tomar como punto de corte el valor pc=0.5, ahora bien tomar esta decisión no quiere decir que sea la solución más óptima como vamos a ver en la exposición que se presenta en lo que resta del post.

Veamos cómo queda si tomamos como punto de corte cp=0.5

cp<-0.5
Yhat<-ifelse(datos$Prob>cp,1,0)
datos$Yhat<-Yhat
head(datos)

##       X Y         Prob Yhat
## 1 -3.83 0 0.0179295281    0
## 2 -2.85 0 0.0495234490    0
## 3 -6.23 0 0.0013978077    0
## 4  8.57 1 0.9999054240    1
## 5 -8.14 0 0.0001812703    0
## 6 -4.93 0 0.0055947128    0

Podemos ahora obtener los herreros que se han cometido con esta clasificación:

errores<-which(datos$Y != datos$Yhat)
nerrores<-length(errores)
print(paste("Numero de errores:",nerrores))

## [1] "Numero de errores: 74"

print(paste("Tasa de errores:",nerrores/nrow(datos)))

## [1] "Tasa de errores: 0.074"

print(paste("Tasa de aciertos:",(1-(nerrores/nrow(datos)))))

## [1] "Tasa de aciertos: 0.926"

Matriz de confusión

Cuando hacemos, como en el presente post, un estudio de clasificación de los datos podemos generar la denominada Matriz de confusión que no es más que una tabla de contingencia, con el formato que se indica a continuación.

		Valores observados
		1	0
Valores estimados	1	VP	FP	P*=VP+FP
	0	FN	VN	N*=FN+VN
		P=VP+FN	N=FP+VN

En la tabla anterior, se ha empleado la siguiente nomenclatura:

VP: Verdaderos positivos. Se estima 1 y el valor es 1
VN: Verdaderos negativos. Se estima 0 y el valor es 0
FN: Falsos negativos. Se estima 0 y verdadero valor es 1
FP: Falsos positivos. Se estima 1 y verdadero valor es 0

De acuerdo con esta nomenclatura se pueden obtener los siguientes indicadores:

Sensibilidad o Razón de Verdaderos Positivos(VPR): VPR=VP/P=VP/(VP+FN)
Especificidad o Razón de Verdaderos Negativos (SPC):SPC=VN/N=VN/(VN+FP)
Ratio o razón de Falsos Positivos (FPR): FPR=FP/(FP+VN)=1-SPC
Exactitud o acuracidad (ACC):ACC=(VP+VN)/(P+N)
Valor Predictivo Positivo o Precisión (PPV): PPV=VP/(VP+FP)
Valor Predictivo negativo (NPV):NPV=VN/(VN+FN)

Para el ejemplo que nosotros tenemos, vamos a crear de forma manual la tala de contingencia correspondiente:

(tContin<-table(datos$Yhat,datos$Y))

##    
##       0   1
##   0 448  35
##   1  39 478

#Para darle el mismo formato que la tabla genérica anterior, hacemos:
print("Reformulando la tabla de contingencia")

## [1] "Reformulando la tabla de contingencia"

(tContin<-table(datos$Yhat,datos$Y)[2:1,2:1])

##    
##       1   0
##   1 478  39
##   0  35 448

Con los datos anteriores, ya se pueden calcular los índices de sensibilidad y especificidad, lo haremos de un forma bien fácil, utilizando la función “prop.table”.

(tContinProporcion<-prop.table(tContin,margin = 2))

##    
##              1          0
##   1 0.93177388 0.08008214
##   0 0.06822612 0.91991786

De esta manera ya tendríamos los valores que buscamos:

sensibilidad<-tContinProporcion[1,1]
especificidad<-tContinProporcion[2,2]
tasaaciertos<-sum(diag(tContin))/(sum(tContin))
print(paste("Valor de sensibilidad: ",sensibilidad))

## [1] "Valor de sensibilidad:  0.9317738791423"

print(paste("Valor de especificidad: ",especificidad))

## [1] "Valor de especificidad:  0.919917864476386"

print(paste("Tasa de aciertos: ",tasaaciertos))

## [1] "Tasa de aciertos:  0.926"

Librerías de R

Para realizar todos los cálculos anteriores de una forma más cómoda, R dispone de librerías que facilitan esta tarea. Entre estas librerías destacan la librería caret y la librería InformationValue. En este post me voy a centrar en la librería caret, pero la mayor parte de los resultados también se pueden obtener con la librería InformationValue.

Con la librería caret para sacar la matriz de confusión, lo primero que hay que hacer es pasar a variables de tipo factor tanto la predicción como los valores observados. Esto es lo primero que hacemos con el siguiente código:

if (!require("caret")) install.packages("caret"); require("caret")

## Loading required package: caret

## Loading required package: lattice

## Loading required package: ggplot2

predicho_f<-factor(datos$Yhat,levels = 1:0)
Y_f<-factor(datos$Y,levels = 1:0)
(MatrizConf<-caret::confusionMatrix(predicho_f,Y_f))

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction   1   0
##          1 478  39
##          0  35 448
##                                          
##                Accuracy : 0.926          
##                  95% CI : (0.908, 0.9415)
##     No Information Rate : 0.513          
##     P-Value [Acc > NIR] : <2e-16         
##                                          
##                   Kappa : 0.8519         
##  Mcnemar's Test P-Value : 0.7273         
##                                          
##             Sensitivity : 0.9318         
##             Specificity : 0.9199         
##          Pos Pred Value : 0.9246         
##          Neg Pred Value : 0.9275         
##              Prevalence : 0.5130         
##          Detection Rate : 0.4780         
##    Detection Prevalence : 0.5170         
##       Balanced Accuracy : 0.9258         
##                                          
##        'Positive' Class : 1              
## 

Ahora se pueden obtener los valores de forma individual.

# Tabla de confusión
MatrizConf$table

##           Reference
## Prediction   1   0
##          1 478  39
##          0  35 448

MatrizConf$byClass

##          Sensitivity          Specificity       Pos Pred Value 
##            0.9317739            0.9199179            0.9245648 
##       Neg Pred Value            Precision               Recall 
##            0.9275362            0.9245648            0.9317739 
##                   F1           Prevalence       Detection Rate 
##            0.9281553            0.5130000            0.4780000 
## Detection Prevalence    Balanced Accuracy 
##            0.5170000            0.9258459

print(paste("Sensitividad: ",MatrizConf$byClass[1]))

## [1] "Sensitividad:  0.9317738791423"

print(paste("Especificidad: ",MatrizConf$byClass[2]  ))

## [1] "Especificidad:  0.919917864476386"

Anteriormente hemos dicho que se tomaba el punto de corte cp en 0.5 por conveniencia, más que por buscar el punto de corte óptimo. Para mejorar este criterio, vamos a definir un función que permita calcular los valores de especificidad, sensitividad y tasa de aciertos, con el fin de utilizarla posteriormente, para poder elegir el punto de corte CP con un criterio de optimización. Veamos cómo definimos esa función.

PuntoCorte = function(glmXY, cp){
  #glmXY es un modelo logit
  #cp es el punto de corte
Y = glmXY$y
clasificacion = ifelse(glmXY$fitted.values > cp, 1, 0)
clasificacion_f = factor(clasificacion, levels = 1:0)
Y_f = factor(Y, levels = 1:0)
confMat = caret::confusionMatrix(clasificacion_f, Y_f)
return(c(confMat$byClass[1], confMat$byClass[2], confMat$overall[1]))
}

Vamos a utilizar la función anterior y comprobar que los resultados que nos dan coinciden con los que ya se na obtenido en pasos anteriores.

PuntoCorte(modelo,cp=0.5)

## Sensitivity Specificity    Accuracy 
##   0.9317739   0.9199179   0.9260000

PuntoCorte(modelo,cp=0.6)

## Sensitivity Specificity    Accuracy 
##   0.9200780   0.9486653   0.9340000

Por lo tanto con la función definida anteriormente, se podría intentar hacer un procedimiento variando el valor de cp, de tal manera que se maximice los valores de sensibilidad y especifidad y acuracidad.

Los valores de la sensibilidad y especificidad, evolucionan de forma contraria respecto al punto de corte CP, de tal manera que al variar cp entre cero y uno si una crece la otra disminuye. Veamos esto en nuestro ejemplo concreto.

cp_v = seq(1, 0, by = -0.001)
sens = sapply(cp_v, FUN = function(cp){PuntoCorte(modelo, cp)[1]})
espec = sapply(cp_v, FUN = function(cp){PuntoCorte(modelo, cp)[2]})
plot(cp_v, sens, type="l", col="red", lwd=3, lty=1, xlab="punto de corte", ylab="")
points(cp_v, espec, type="l", col="blue", lwd=3, lty=2)
legend(x="bottom", legend=c("sensibilidad", "especificidad"),
col = c("red", "blue"), bty=1, lty=c(1,2),lwd=3)

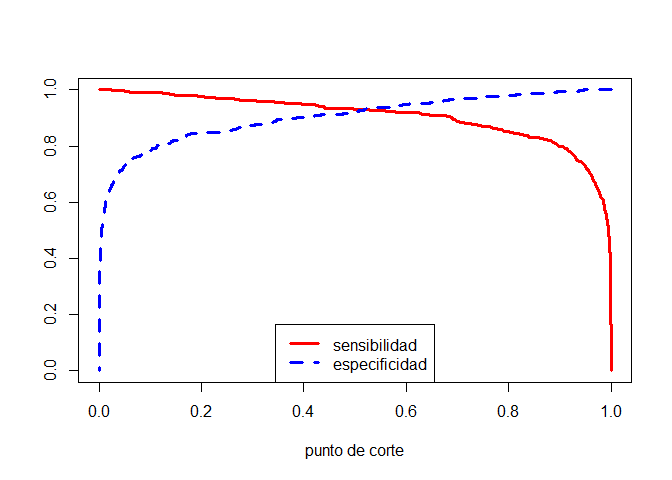
En vista de la figura anterior se podría pensar en utilizar como punto de corte el punto donde se cruzan ambas curvas. Veamos cómo calcularíamos ese punto.

dif<-abs(sens-espec)
a<-which.min(dif)
cp_v[a]

## [1] 0.521

La librería InformationValue también nos ofrece una función para poderla utilizar y definir ese punto de corte. Esta función tiene el parámetro optimiseFor para utilizar diferentes criterios de optimización. Veamos cómo poder utilizar este criterio.

if (!require("InformationValue")) install.packages("InformationValue"); require("InformationValue")

## Loading required package: InformationValue

## 
## Attaching package: 'InformationValue'

## The following objects are masked from 'package:caret':
## 
##     confusionMatrix, precision, sensitivity, specificity

optimalCutoff(datos$Y,datos$Prob)

## [1] 0.5999795

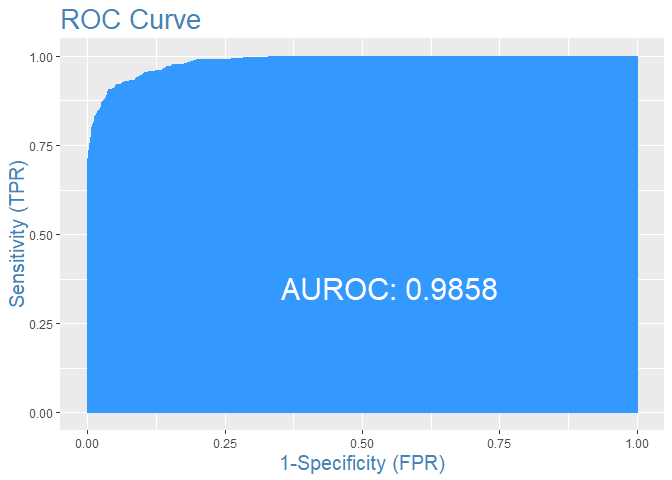
Curva de ROC

Una de las funciones más utilizadas en problemas de clasificación es la curva de ROC, cuya área que determina con los ejes de abscisas nos permite evaluar la fiabilidad de la clasificación. Esta curva por ejemplo puede ser de mucha utilidad, si se quieren comparar dos o más modelos de clasificación. Esta curva se construye de la siguiente manera.

Los valores tanto en el eje de abscisas como de ordenadas van a estar entre cero y uno. En el eje de abscisas, se va a colocar el valor de 1-especificidad, y en el de ordenadas el valor de la sensibilidad. Como ya hemos visto para cada valor del punto de corte se obtiene un valor de especificidad y otro de sensibilidad. Entonces hacemos variar el punto de corte entre cero y uno y ya tenemos los pares de valores necesarios para construir la curva de ROC. Con los cálculos que se han hecho anteriormente, la representación de la curva de ROC es muy fácil:

plot(1- espec, sens, type = "l", col="blue", lwd=4,
xlab="1 - especificidad", ylab="sensibilidad",
xlim=c(0, 1), ylim=c(0, 1), asp=1)
polygon(c(0, 0, 1, 1), c(0, 1, 1, 0), lwd=2)
segments(x0 = 0, y0 = 0, x1 = 1, y1 = 1, col="black", lty=2, lwd=4)

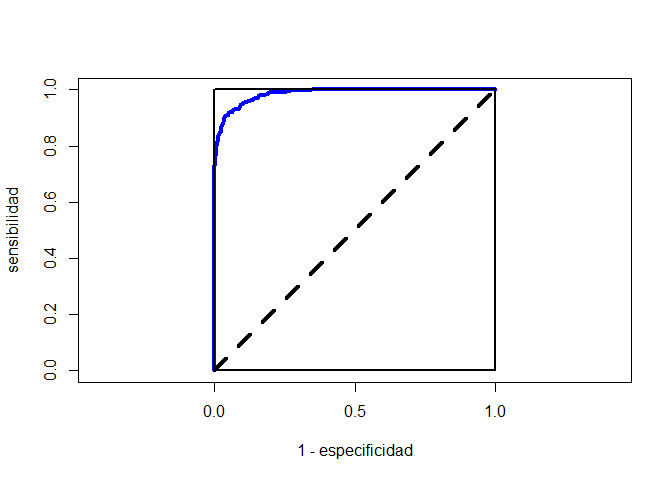
La librería ROCR nos permite dibujar de una forma cómoda la curva de ROC del ejemplo. Se utiliza la función prediction de esa librería para que haga sus cálculos y así pueda dibujar dicha curva

if (!require("ROCR")) install.packages("ROCR"); require("ROCR")

## Loading required package: ROCR

## Loading required package: gplots

## 
## Attaching package: 'gplots'

## The following object is masked from 'package:stats':
## 
##     lowess

preLog<-prediction(predictions = modelo$fitted.values ,labels = datos$Y)
#La función perfomance nos permite obtener muchos valores para el análisi
ROC<-performance(preLog,measure = "tpr",x.measure = "fpr")
#Paámetros para que la curva de ROC quede corecta
par(mar=c(5,5,2,2),xaxs = "i",yaxs = "i",cex.axis=1.3,cex.lab=1.4)
plot(ROC)
abline(a=0, b= 1)

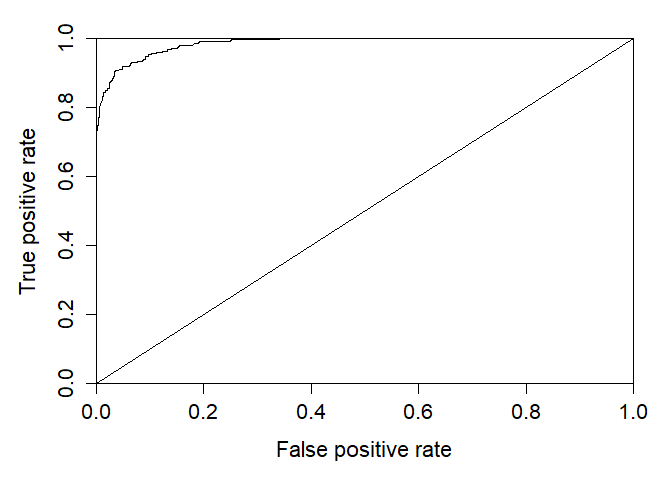Observamos que la curva obtenida es la misma que cuando se ha obtenido de forma manual. De interés es el área debajo de curva con los ejes coordenados. Veamos cómo obtenerla con estos métodos.

AUC<-performance(preLog,"auc")
print("El área sería: ")

## [1] "El área sería: "

AUC@y.values

## [[1]]
## [1] 0.9859145

La librería InformationValue también nos permite obtener la curva de ROC, así como su área. A continuación se muestra cómo se haría en este caso.

plotROC(datos$Y,modelo$fitted.values)

Descargar fichero *.Rmd

Descargar fichero datos

Técnicas de Big Data