Regresión Logit (I)
Contenido
Introducción
En este post se va a hacer una presentación de la metodología a utilizar en el caso de que se quiera hacer un tipo de regresión donde la variable independiente es de tipo cualitativo, y más en concreto binaria ( de forma fácil lo que aquí se exponga se puede extender a variables de tipo multinomial ).
Así pues nos centraremos en variables dicotómicas, por ejemplo que una persona tenga una determinada enfermedad, en cuyo caso se asignará el valor 1 si se tiene la enfermedad y 0 en caso contrario. En este tipo de regresión, las variables independientes pueden ser continuas o categóricas.
En principio hay que aclarar que el modelo de regresión a utilizar no puede ser el que se utiliza en la regresión lineal con carácter general, ya que ese modelo predice valores que en absoluto van a estar dentro del rango entre 0 y 1.
Para ir entrando en materia, vamos a utilizar un fichero con solo dos variables (es decir, columnas). Una columna denominada Vasculopatia ( Término general empleado para describir cualquier trastorno de los vasos sanguíneos), y la otra denominada ITB( Indice Tobillo Brazo, que es la relación entre la tensión arterial sistólica medida en el tobillo y la medida en la arteria braquial). La primera va a ser la variable independiente y la segunda la variable dependiente.
Carguemos inicialmente el fichero como un data set de R.
datos<-read.csv("./data/DatosVasculopatia.csv", header = T,sep=",")
head(datos)
## ITB Vasculopatia
## 1 0.94 0
## 2 0.99 0
## 3 0.88 1
## 4 0.64 1
## 5 1.25 0
## 6 0.50 1
Con el fin de mejorar la claridad expositiva del post, vamos a llamar “Y”” a la variable independiente (ITB) y “X” a la variable dependiente (Vasculopatia).
colnames(datos)<-c("X","Y")
colnames(datos)
## [1] "X" "Y"
A continuación procedemos a hacer una representación gráfica de los datos, así como un ajuste de regresión lineal.
colores = c()
colores[datos$Y == 0] = "darkgoldenrod"
colores[datos$Y == 1] = "deepskyblue4"
plot(datos$X, datos$Y, pch = 21, bg = colores, cex=1.3,font=2,
xlab = "Indice tobillo brazo", ylab = "Vasculopatia", font.lab=2, )
legend("left", c("No vasculopatía", "Vasculopatía"), pch = 21,
pt.bg = c("darkgoldenrod", "deepskyblue4"))
rg<-lm(Y~X,data = datos)
abline(rg, col="red",lwd=3 )
text(1.1,0.4,labels = c("Línea de regresión"))
box(lwd=3)
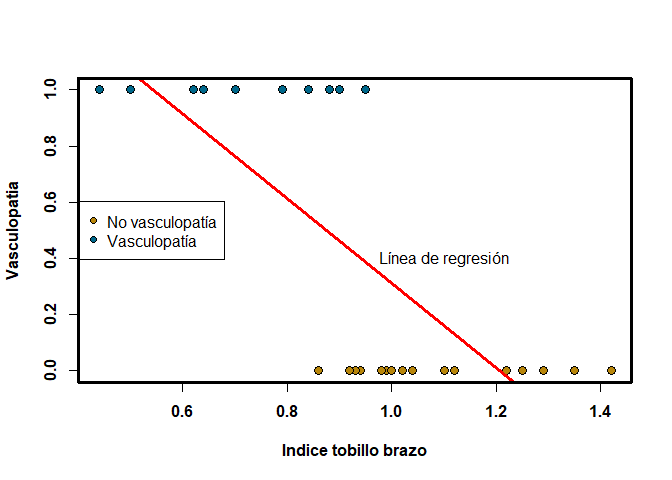
Como se puede ver en el gráfico anterior, indudablemente en estos casos no es en absoluto aconsejable ni conveniente utilizar un modelo de regresión lineal. Veamos cómo se enfoca el modelo para esto. Antes de entrar en materia vamos a ver qué se entiende por odds, término muy utilizado en este tipo de regresión. Observar además, que tal y como están construidos los odds pueden tomar valores entre cero e infinito.
El término “Odds” está muy ligado al de probabilidad y se define como el cociente entre el número de éxitos y el número de fracasos. Es decir, si p es la probabilidad de tener 1 y q=1-p es la probabilidad de tener cero en una variable binomial, entonces:
\[ odds=\frac{p}{q}=\frac{p}{1-p} \]
Veamos a continuación cual es la relación existente entre el concepto de probabilidad y odds. Por la letra O vamos a representar a los odds.
\[ O=\frac{p}{1-p} \; entonces \; O-Op=p \; \Rightarrow \; O=p+Op=p(1+O) \Rightarrow p=\frac{O}{1+O} \]
Una vez hecha esta pequeña introducción, a continuación nos vamos a centrar en la forma en que se construye el modelo.
Construcción del modelo
Como ya se ha dicho en el apartado anterior, no se puede utilizar un modelo de regresión lineal, para hacer un ajuste de una variable dependiente dicotómica. Se podría pensar que ese modelo, se hiciera sobre el valor de la probabilidad de que esa variable tomara el valor de 1, es decir sobre p[Y=1]=p. Pero con este planteamiento estaríamos exactamente en la misma situación que lo comentado en el caso anterior.
La cosa cambia un poco, si en lugar de tomar p tomamos lo que anteriormente hemos denominado odds, pues en este caso estamos hablando de un indicador que toma valores entre cero e infinito. No obstante en este caso también pudiera ocurrir que el modelo de regresión lineal que se construye pudiera tomar valores negativos y entonces tampoco serviría.
Para solucionar todos estos problemas, lo que se hace es tomar el logaritmo de los odds, y en este caso ya sí tendríamos resuelto el problema que teníamos con las consideraciones expuestas anteriormente, ya que en este caso los valores que tomaría la variable dependiente sería valores entre menos infinito y más infinito. Por lo tanto al modelo con el que se deberá trabajar, será el siguiente:
\[ ln(\frac{p}{1-p})=b_0+b_1X_1+b_2X_2+\cdots +b_nX_n+e=Xb+e \]
Con el fin de simplificar las expresiones que se van a utilizar posteriormente vamos a llamar Z a la siguiente expresión:
\[ Z=b_0+b_1X_1+b_2X_2+\cdots +b_nX_n \]
y por lo tanto el modelo que quedaría sería el siguiente:
\[ ln(\frac{p}{1-p})=Z+e\]
Operemos sobre la expresión anterior para calcular p en función de z \[ ln(\frac{p}{1-p})=Z\: \Rightarrow \frac{p}{1-p}=e^Z\:\Rightarrow p=e^Z(1-p) \]
\[ p+pe^Z=e^Z \:\Rightarrow p(1+e^Z)=e^Z \:\Rightarrow p=\frac{e^Z}{1+e^Z}=\frac{1}{1+e^{-z}} \]
A continuación representamos la función
\[ F(x)=\frac{1}{1+e^{-x}} \]
x=seq(-10,10,0.1)
y=1/(1+exp(-x) )
plot(x,y,type = 'l',main = ('Representación de la función '~(1/e^-x)))
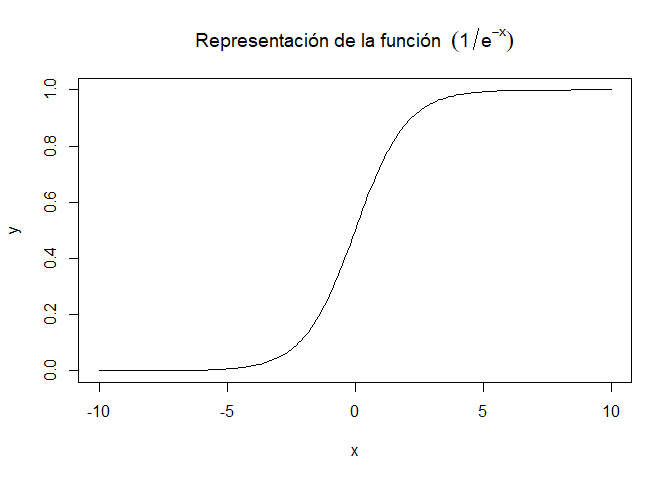
Como se puede ver en la gráfica anterior F(x) realmente es una función de distribución, en concreto es la función de distribución de variable logística. Por lo tanto, realmente el ajuste que finalmente se hace es el que se corresponde a la siguiente ecuación:
p(a/x)=F(x * b)
Donde F es una función de distribución, que para estos casos puede ser:
1.- Una función de distribución logística. Y entonces tendremos una regresión logit
2.- Una función de distribución de una normal. Y entonces tendremos una Regresión Probit
En lo que sigue me centraré en el modelo de regresión logit que es el más utilizado.
En las expresiones anteriores se tiene:
\[ ln(\frac{p}{1-p})=Z \: \Rightarrow ln(p)-ln(1-p)=Z=b_0+b_1X_1+\cdots +b_nX_n \]
De lo que se deduce que la diferencia de probabilidad de que ocurra un suceso respecto de que ocurra el contrario es lineal, pero en este caso en escala logarítmica. Por lo tanto en esta caso los coeficientes, en principio, serán, más difíciles de interpretar que en el caso de un ajuste de regresión normal.
Dos fórmulas que conviene recordar por su frecuencia de uso en el modelo de regresión logit son las siguientes:
\[ ln(p)-ln(1-p)=b_0+b_1X_1+\cdots +b_nX_n \] \[ \frac{p}{1-p}=e^{b_0+b_1X_1+\cdots +b_nX_n}=e^b_0*e^{b_1X_1}*\cdots*b_nX_n \]
Hay que recordar también que:
\[ p=\frac{1}{1+e^{-{(b_0+e^{b_1X_1}+\cdots+b_nX_n)}}} \]
La estimación de los parámetros se realiza en este caso mediante el método de máxima verosimilitud, y no mediante el método de mínimos cuadrados como ocurría en el caso de la regresión lineal.
Interpretación de los parámetros.
Como ya se ha visto la interpretación de los valores de los parámetros del modelo, no tienen una interpretación tan sencilla como en el caso del modelo de regresión lineal múltiple. En este apartado vamos a ver qué conclusiones se pueden sacar de los mismos.
Ya hemos visto anteriormente que
\[ O_i=\frac{p_i}{1-p_i}=exp(b_0)\prod_{j=1}^{n}{exp(b_j)^{x_j}} \]
Entonces vamos a suponer que para el primer elemento tenemos los siguientes valores (Xi1, Xi2, ⋯, Xi**h, ⋯, Xi**n) Y por otro lado tenemos otra observación con los siguientes valores (Xj1, Xj2, ⋯, Xj**h, ⋯, Xj**n) Y ahora como es normal en este tipo de situación supongamos que todos los valores son iguales en las dos observaciones, salvo para la variables que ocupa la posición h que verifica lo so siguiente: ( X_{ih}=X_{jh}+1 ), en esta ocasión al hacer el cociente de los Odds correspondientes se simplicarán todos los términos del producto salvo el que ocupa la posición h, y por lo tanto quedará lo siguiente:
\[ \frac{O_i}{O_j}=e^{b_h} \]
y por lo tanto \( e^{b_h} \) indicará cuánto se modifica el ratio de probabilidades cuando las variable \( X_h \) se incrementa en una unidad.
Lo anterior es válido en el caso de que se tenga una variable de tipo continuo. Sin embargo cuando se tiene una variable de tipo categórico, el valor de \( e^{b_h} \) indicará el incremento en el ratio de probabilidades de pasar de una categoría de referencia a otra a la que hace referencia el parámetro obtenido.
Un primer ejemplo
Para ir entrando en materia, vamos a utilizar R para resolver el ajuste en los datos que hemos introducido anteriormente, es decir ver la influencia que la variable “Indice tobillo brazo”(ITB) sobre la variable “Vasculopatía”. Para hacer esto utilizamos la función glm (generalize lineal model) de R que juega un papel parecido con respecto a los modelos lineales generalizados, de los que la regresión logística es un ejemplo. Utilizaremos el siguiente código:
(glmXY = glm(Y ~ X, family = binomial(link = "logit"), data = datos))
##
## Call: glm(formula = Y ~ X, family = binomial(link = "logit"), data = datos)
##
## Coefficients:
## (Intercept) X
## 29.98 -33.13
##
## Degrees of Freedom: 29 Total (i.e. Null); 28 Residual
## Null Deviance: 39.43
## Residual Deviance: 12.53 AIC: 16.53
Con los resultados obtenidos anteriormente tenemos mayoritariamente definido el modelo en sus aspectos fundamentales, pero si queremos obtener una información más pormenorizada, debemos utilizar el comando summary(), vemos los resultados que se obtienen con él.
summary(glmXY)
##
## Call:
## glm(formula = Y ~ X, family = binomial(link = "logit"), data = datos)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.83736 -0.26883 -0.00464 0.01636 1.84403
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 29.98 14.44 2.077 0.0378 *
## X -33.13 15.78 -2.100 0.0357 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 39.429 on 29 degrees of freedom
## Residual deviance: 12.534 on 28 degrees of freedom
## AIC: 16.534
##
## Number of Fisher Scoring iterations: 8
Como puede verse en la salida anterior, la cantidad de información se incrementa considerablemente al usar la función summary. En el caso de la tabla Coefficients la columna Estimate refleja los parámetros \( b_j\) que ha estimado el modelo. Estos mismos coeficientes, de forma aislada se pueden obtener de la siguiente manera:
glmXY$coefficients
## (Intercept) X
## 29.97863 -33.13386
Y nos podremos referir a ellos de forma individual de la siguiente manera:
(b0<-glmXY$coefficients[1])
## (Intercept)
## 29.97863
(b1<-glmXY$coefficients[2])
## X
## -33.13386
A continuación vamos a añadir la curva logística obtenida a la representación de los datos, pero antes conviene que recuerdes la fórmula siguiente, para entender mejor la representación que se hace:
\[ p=\frac{1}{1+e^{-{(b_0+e^{b_1X_1}+\cdots+b_nX_n)}}}=\frac{e^{(b_0+e^{b_1X_1}+\cdots+b_nX_n)}}{1+ e^{(b_0+e^{b_1X_1}+\cdots+b_nX_n)}} \]
curvaLogit<-function(x){
return(exp(b0+b1*x)/(1+exp(b0+b1*x)))
}
curve(curvaLogit,from = -10, to=10, col="blue",lwd="2")
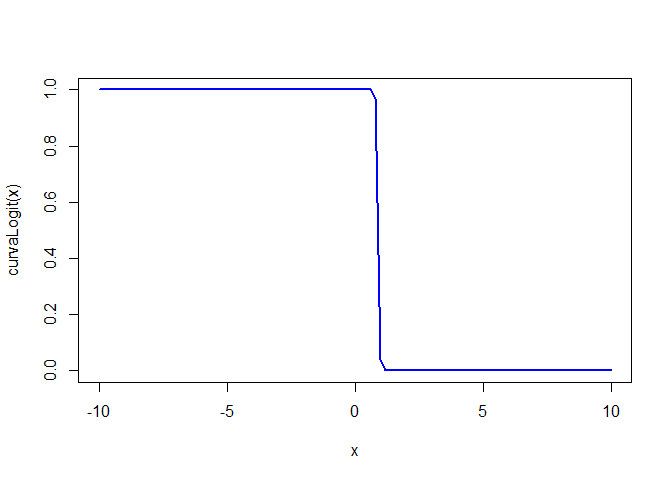
Como ya hemos comentado anteriormente, la estimación de los parámetros se hace mediante el método de máxima verosimilitud. R permite obtener el logaritmo de esa máxima verosimilitud de la siguiente manera.
(logVerisimilitud<-logLik(glmXY))
## 'log Lik.' -6.266752 (df=2)
Y para calcular exactamente la verosimilitud, se hará lo siguiente:
(Verosimilitud<-exp(logLik(glmXY)[1]))
## [1] 0.001898385
En este ejemplo concreto veamos la predicción de probabilidad que nos da este modelo para cada uno de los datos utilizados para este ejemplo:
pred<-glmXY$fitted.values
head(pred)
## 1 2 3 4 5
## 2.373616e-01 5.604664e-02 6.944130e-01 9.998452e-01 1.077041e-05
## 6
## 9.999985e-01
Ahora pongamos estos valores ( que recordemos son probabilidades ) junto con los datos iniciales
datosFinal<-cbind(datos,pred)
head(datosFinal)
## X Y pred
## 1 0.94 0 2.373616e-01
## 2 0.99 0 5.604664e-02
## 3 0.88 1 6.944130e-01
## 4 0.64 1 9.998452e-01
## 5 1.25 0 1.077041e-05
## 6 0.50 1 9.999985e-01
La columna pred contiene las probabilidades estimadas de que la variable Y tomo el valor 1. Vemos que en el primer caso esa probabilidad es muy escasa, lo mismo que en el segundo, por lo que en el caso de hacer una clasificación, los dos primeros casos los clasificaríamos como Y=0. in embargo en el tercer caso , la probabilidad de que Y=1 es mayor que 0,5 por lo que en un principio asignaríamos a esta observación en la clase Y=1. Este sistema por lo tanto nos podría servir como una herramienta de clasificación de observaciones, aunque indudablemente puede presentar una sensible mejoría.
Un vez construido el modelo, lo podemos usar para calcular predicciones, que en este caso realmente son probabilidades. Veamos cómo se haría.
f=0.85
predict(glmXY,newdata=data.frame(X=f) )
## 1
## 1.814848
Observar que realmente hemos obtenido una probabilidad pues el valor es mayor que 1. Realmente lo que se obtiene es el valor de \( b_0+b_1X_1+… +b_nX_n \), lo cual se comprueba a continuación.
b0+b1*f
## (Intercept)
## 1.814848
Para obtener realmente la probabilidad debemos poner lo siguiente:
predict(glmXY,newdata=data.frame(X=f) ,type = "response" )
## 1
## 0.8599468
Para mejorar la exposición que sigue, vamos a recordar los datos que obtenemos con este modelo.
(sum1<-summary(glmXY)$coefficients)
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 29.97863 14.43516 2.076779 0.03782199
## X -33.13386 15.77522 -2.100374 0.03569591
En esta tabla y en concreto en la segunda columna se muestra la desviación típica del estimador, y en la tercera columna se puede ver el estadístico de Wald que se define como
\[ W(b_j)=\left [\frac{b_j}{\sigma(b_j)} \right ]^{2} \]
El estadístico de Wald sigue una chi-cuadrado con un grado de libertad, por lo tanto su raíz cuadrada seguirá una distribución normal estándar. Precisamente los valores que figuran en la tercera columna son las raíces cuadradas del estadístico de Wald, como se puede ver a continuación.
(wb1<-sum1[1,1]/sum1[1,2])
## [1] 2.076779
(Wb2<-sum1[2,1]/sum1[2,2])
## [1] -2.100374
Los valores de la cuarta columna son los p-values del contraste de hipótesis ( b_i=0), veamos cómo se calculan estos valores.
(p1=2*(pnorm(abs(sum1[1,3]),lower.tail = F)))
## [1] 0.03782199
(p2=2*(pnorm(abs(sum1[2,3]),lower.tail = F)))
## [1] 0.03569591
Deviance.
Entre los resultados obtenidos cuando se ha creado el modelo, está la denominada **Deviance* que se define como D(modelo)=-2ln(verosimilitud(modelo))*. La deviance del modelo se puede calcular de forma fácil así:
glmXY$deviance
## [1] 12.5335
Anteriormente ya se ha dicho cómo se puede calcular el logaritmo de la verosimilitud mediante la función logLik, por lo tanto la deviance, también se calcularía de la siguiente manera:
-2*logLik(glmXY)[1]
## [1] 12.5335
Si observamos los resultados del análisis de regresión obtenidos anteriormente, se puede ver que se obtienen dos tipos de resultados para la deviance:
1.- null deviance
2.- residual deviance
El primero nos devuelve la deviance cuando el modelo sólo considera el primer parámetro ( es decir \( b_0 \) ), este valor también se puede obtener de la siguiente manera:
glmXY$null.deviance
## [1] 39.42947
El valor de residual deviance muestra la deviance del modelo completo. Estos valores de la deviance nos van a servir para formular contrastes de hipótesis sobre los parámetros del modelo,en esta caso en concreto calcularemos el siguiente valor
(h<-glmXY$null.deviance- glmXY$deviance)
## [1] 26.89596
(pvalue<-pchisq(h,lower.tail = F,df=1)) #Pues se distribuye como una chi con 1 grado libertad
## [1] 2.14707e-07
En este caso el p-value obtenido es menor que 0.05 y se rechazaría la hipótesis nula ( ( b_1=0 ) )
De forma general, para hacer este tipo de contrastes, supongamos que tenemos las siguientes hipótesis de contraste :
H0 b1 = b2 = … = bn = 0 H1 ∃ bp ≠ 0
En este caso se calculará el valor de la diferencia de deviances es decir
C2LL* = −2*LL(b0)−(−2l**l(b0, b1, …, bn))
Esta diferencias de logaritmos de verosimilitud se distribuye como una chi-2 con j grados de libertad, done j es la diferencia del número de parámetros del modelo.
Los intervalos de confianza para los parámetros del modelo, se obtendrían de la siguiente manera:
confint.default(glmXY,level=0.95)
## 2.5 % 97.5 %
## (Intercept) 1.686238 58.271023
## X -64.052718 -2.215006
Veamos cómo construir estos intervalos de forma manual.Primero recordemos lo siguiente:
(sum1<-summary(glmXY)$coefficients)
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 29.97863 14.43516 2.076779 0.03782199
## X -33.13386 15.77522 -2.100374 0.03569591
Procedemos ahora a calcular el intervalo del término independiente.
nc=0.95
alfa=1-nc
alfaMedios=alfa/2
zalafaMedios=qnorm(1-alfaMedios)
(b0=sum1[1,1])
## [1] 29.97863
(b1=sum1[2,1])
## [1] -33.13386
(SE_b0=sum1[1,2])
## [1] 14.43516
(SE_b1=sum1[2,2])
## [1] 15.77522
print("Intervalo confianza b0")
## [1] "Intervalo confianza b0"
(intervalo_b0=b0+c(-1,1)*zalafaMedios*SE_b0)
## [1] 1.686238 58.271023
print("Intervalo confianza b1")
## [1] "Intervalo confianza b1"
(intervalo_b1=b1+c(-1,1)*zalafaMedios*SE_b1)
## [1] -64.052718 -2.215006
Medidas de bondad de ajuste.
Al igual que en el modelo de regresión lineal, se puede calcular el valor de ( R^2 ) para evaluar a priori la bondad del ajuste, en el caso de la regresión logit se tienen otros estadísticas para evaluar esa calidad. A continuación se muestran las instrucciones correspondientes y los resultados obtenido
if (!require("rcompanion")) install.packages("rcompanion"); require("rcompanion")
## Loading required package: rcompanion
nagelkerke(glmXY)
## $Models
##
## Model: "glm, Y ~ X, binomial(link = \"logit\"), datos"
## Null: "glm, Y ~ 1, binomial(link = \"logit\"), datos"
##
## $Pseudo.R.squared.for.model.vs.null
## Pseudo.R.squared
## McFadden 0.682128
## Cox and Snell (ML) 0.592018
## Nagelkerke (Cragg and Uhler) 0.809496
##
## $Likelihood.ratio.test
## Df.diff LogLik.diff Chisq p.value
## -1 -13.448 26.896 2.1471e-07
##
## $Number.of.observations
##
## Model: 30
## Null: 30
##
## $Messages
## [1] "Note: For models fit with REML, these statistics are based on refitting with ML"
##
## $Warnings
## [1] "None"
De momento con esto finalizo por ahora la exposición del modelo logit, en post’s posteriores expondré modelos más complejos que el que se ha visto aquí, e igualmente se verá la utilidad de estos modelos para resolver los problemas de clasificación.
