Regresión Logística
Contents
3. Regresión Logística#
3.1. Introducción#
Como ya se sabe, los modelos de regresión tienen como objeto predecir cómo afectan una o más variables explicativas (también llamadas independientes o features), sobre una variable respuesta. Cuando la variable respuesta es de tipo cuantitativo continuo se utiliza como norma general el método de mínimo cuadrados ordinarios para estimar los parámetros del modelo resultante.
Ahora bien, ese método de resolver el problema no sirve cuando la variable respuesta es de tipo discreta (toma pocos valores), y normalmente se trata de una variable categórica con dos o más valores como atributos o categorías. En estos casos los modelos de regresión más utilizados son los denominados modelos de regresión logística y los de tipo Softmax, en los cuales las variables independientes o explicativas, pueden ser de tipo cuantitativo o cualitativo.
En el caso de los modelos cuya variable respuesta sólo puede tomar dos valores, estaríamos ante los denominados modelos de regresión logit o logística a los cuales se les va a dedicar este apartado. A continuación exponemos de forma resumida el aparato teórico, sobre el que se sostenta este modelo.
Supongamos una variable Y que sólo puede tomar dos valores 1 ó 0, y sea un conjunto de variables independientes que denotamos por \(X={x_1,x_2, ...,x_n}\). Llamamos p a la probabilidad de que la variable aleatoria (en adelante v.a.) Y tome el valor 1 suponiendo que se haya obtenido un valor concreto para la v.a. X. Entonces el siguiente modelo de regresión:
No serviría, pues inicialmente ese modelo de regresión no daría valores entre cero y uno que son los valores que puede tomar una probabilidad como p. Entonces, para poder resolver esto, lo que se suele hacer es hacer el siguiente ajuste.
Y en este caso sí tendría sentido hace ese ajuste de regresión. Ahora bien, si en la expresión anterior, se despeja p, nos quedaría la siguiente expresión:
La expresión que tenemos a la derecha de la fórmula anterior se denomina función sigmoidea, y para ver qué formato presenta, a continuación se muestra un trozo de código, que permite hacer una representación gráfica de la función.
import math
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(x):
a = []
for item in x:
a.append(1/(1+math.exp(-item)))
return a
plt.figure(figsize=(16,7))
plt.title("Gráfica de la función sigmoidea")
x = np.arange(-10., 10., 0.2)
sig = sigmoid(x)
plt.plot(x,sig)
plt.show()
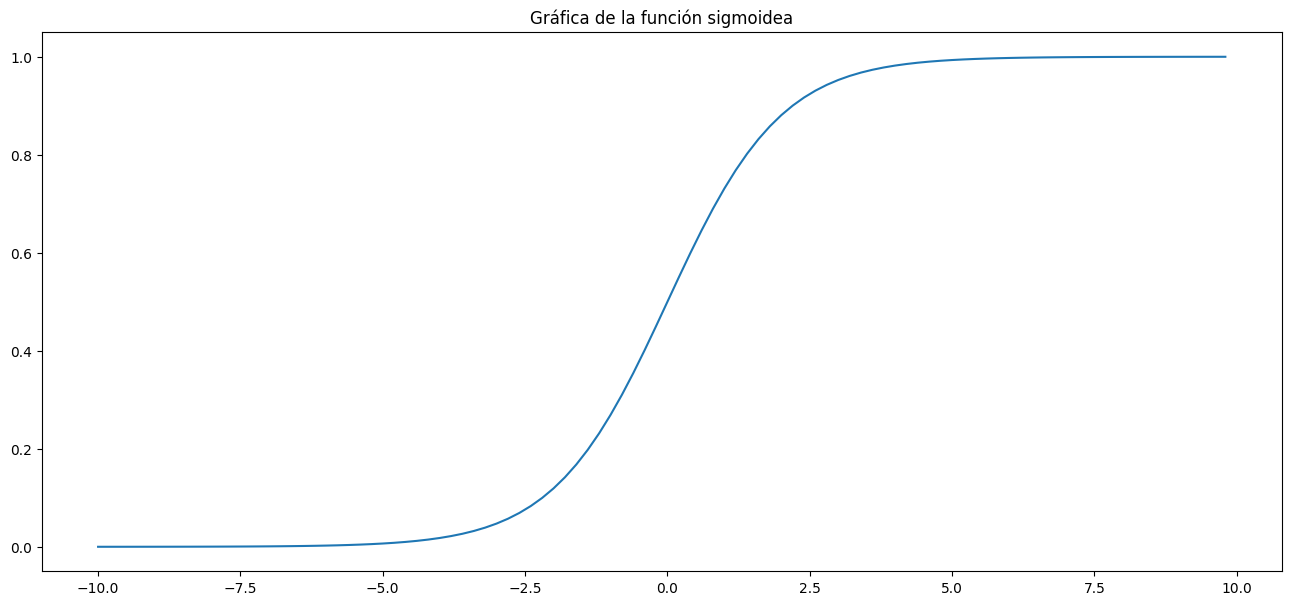
Como puede verse en la figura, la función sigmoidea, verifica las siguientes propiedades:
1.- Es una función monótana creciente en todo su dominio de definición.
2.- Tiene dos asíntotas horizontales, una situada en el punto cero y otra en el punto 1.
Todas estas propiedades vista hasta este momento, son las que nos van a permitir poder hacer las correspondientes clasificaciones en el caso de tener una variable aleatoria independiente dicotómica. En este sentido, si el valor que nos da el modelo es inferior a 0.5 clasificaríamos en punto en cuestión como de la clase 0 (se asume que el modelo presenta dos modalidades que denominamos 0 ó 1) y en caso contrario se clasificará en la otra clase.
Es preciso matizar que este punto de corte normalmente tienen por denominación cutoff (o también Thershold) y que no siempre se toma el punto 0.5 como referencia de corte, sino se utilizan diferentes procedimientos para obtener este punto de tal manera que se cometa el menor error posible.
En este enlace https://stackoverflow.com/questions/28719067/roc-curve-and-cut-off-point-python, se puede ver algún método de cómo elegir ese punto de corte con la finalidad de mejorar la fiabilidad de las predicciones del modelo.
3.2. Primer ejemplo sobre regresión logística#
A continuación procedemos a ver un ejemplo práctico sobre cómo poder utilizar esta metodología a un caso concreto, que ademas podemos encontrar en kaggle. Se trata de estudiar la existencia de posibles fraudes en la utilización de las tarjetas de crédito, en base a la información que facilita otra serie de variables observadas en la práctica diaria.
Para desarrollar este ejemplo, utilizaremos la clase LogisticRegression que pone a nuestra disposición scikit learn.
Carguemos inicialmente los módulos que vamos a utilizar en el desarrollo del problema
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.metrics import roc_curve, roc_auc_score, classification_report, accuracy_score, confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
# leemos los datos
dat = pd.read_csv('data/creditcard.csv')
---------------------------------------------------------------------------
FileNotFoundError Traceback (most recent call last)
Input In [3], in <cell line: 3>()
1 # leemos los datos
----> 3 dat = pd.read_csv('data/creditcard.csv')
File D:\programas\Anaconda\envs\py39\lib\site-packages\pandas\util\_decorators.py:311, in deprecate_nonkeyword_arguments.<locals>.decorate.<locals>.wrapper(*args, **kwargs)
305 if len(args) > num_allow_args:
306 warnings.warn(
307 msg.format(arguments=arguments),
308 FutureWarning,
309 stacklevel=stacklevel,
310 )
--> 311 return func(*args, **kwargs)
File D:\programas\Anaconda\envs\py39\lib\site-packages\pandas\io\parsers\readers.py:680, in read_csv(filepath_or_buffer, sep, delimiter, header, names, index_col, usecols, squeeze, prefix, mangle_dupe_cols, dtype, engine, converters, true_values, false_values, skipinitialspace, skiprows, skipfooter, nrows, na_values, keep_default_na, na_filter, verbose, skip_blank_lines, parse_dates, infer_datetime_format, keep_date_col, date_parser, dayfirst, cache_dates, iterator, chunksize, compression, thousands, decimal, lineterminator, quotechar, quoting, doublequote, escapechar, comment, encoding, encoding_errors, dialect, error_bad_lines, warn_bad_lines, on_bad_lines, delim_whitespace, low_memory, memory_map, float_precision, storage_options)
665 kwds_defaults = _refine_defaults_read(
666 dialect,
667 delimiter,
(...)
676 defaults={"delimiter": ","},
677 )
678 kwds.update(kwds_defaults)
--> 680 return _read(filepath_or_buffer, kwds)
File D:\programas\Anaconda\envs\py39\lib\site-packages\pandas\io\parsers\readers.py:575, in _read(filepath_or_buffer, kwds)
572 _validate_names(kwds.get("names", None))
574 # Create the parser.
--> 575 parser = TextFileReader(filepath_or_buffer, **kwds)
577 if chunksize or iterator:
578 return parser
File D:\programas\Anaconda\envs\py39\lib\site-packages\pandas\io\parsers\readers.py:934, in TextFileReader.__init__(self, f, engine, **kwds)
931 self.options["has_index_names"] = kwds["has_index_names"]
933 self.handles: IOHandles | None = None
--> 934 self._engine = self._make_engine(f, self.engine)
File D:\programas\Anaconda\envs\py39\lib\site-packages\pandas\io\parsers\readers.py:1218, in TextFileReader._make_engine(self, f, engine)
1214 mode = "rb"
1215 # error: No overload variant of "get_handle" matches argument types
1216 # "Union[str, PathLike[str], ReadCsvBuffer[bytes], ReadCsvBuffer[str]]"
1217 # , "str", "bool", "Any", "Any", "Any", "Any", "Any"
-> 1218 self.handles = get_handle( # type: ignore[call-overload]
1219 f,
1220 mode,
1221 encoding=self.options.get("encoding", None),
1222 compression=self.options.get("compression", None),
1223 memory_map=self.options.get("memory_map", False),
1224 is_text=is_text,
1225 errors=self.options.get("encoding_errors", "strict"),
1226 storage_options=self.options.get("storage_options", None),
1227 )
1228 assert self.handles is not None
1229 f = self.handles.handle
File D:\programas\Anaconda\envs\py39\lib\site-packages\pandas\io\common.py:786, in get_handle(path_or_buf, mode, encoding, compression, memory_map, is_text, errors, storage_options)
781 elif isinstance(handle, str):
782 # Check whether the filename is to be opened in binary mode.
783 # Binary mode does not support 'encoding' and 'newline'.
784 if ioargs.encoding and "b" not in ioargs.mode:
785 # Encoding
--> 786 handle = open(
787 handle,
788 ioargs.mode,
789 encoding=ioargs.encoding,
790 errors=errors,
791 newline="",
792 )
793 else:
794 # Binary mode
795 handle = open(handle, ioargs.mode)
FileNotFoundError: [Errno 2] No such file or directory: 'data/creditcard.csv'
Veamos a grandes pinceladas su contenido:
dat.head()
te fichero. También existe el campo denominado class con valores cero y uno para indicar se ha habido o no fraude en la utilización de la tarjeta.
Veamos cómo están distribuidos los datos, y en especial los casos que hay de fraude o no fraude, para ello procedemos a realizar a hacer un simple diagrama de barras de la variable class
f, ax = plt.subplots(figsize=(12, 5))
sns.countplot(x='Class', data=dat)
_ = plt.title('Casos de fraude y no fraude')
_ = plt.xlabel('1= si fraude; 0 = No fraude')
Observamos que estamos claramente ante un caso de datos no balanceados, lo cual puede suponer un problema a la hora de generar el modelo. Existen diversas formas para solventar este problema, y en este ejemplo, lo que se va a aplicar es el parámetro “class_weight” de la clase LogisticRegression, que si miramos en la documentación de scikit learn lo que hace es asignar diferentes pesos a las observaciones.
En concreto, si asignamos a este parámetro el valor de “balanced”, entonces toma el valor de la variables dependiente para hacer el ajuste de forma inversamente proporcional al número de caso que tiene cada categoría de esta variable, en concreto los pesos los calcula de acuerdo a la siguiente expresión: n_samples / (n_classes * np.bincount(y))
En el resultado mostrado en la celda siguiente podemos observar que el 99.8 por ciento de la transacciones son no fraudulentas y por consiguiente el nivel de datos no balanceados es importante.
(dat.Class.value_counts()[0]/len(dat))*100
X = dat.drop(columns='Class', axis=1)
y = dat.Class.values
np.random.seed(100)
X_train, X_test, y_train, y_test = train_test_split(X, y)
scalar = StandardScaler()
#lr = LogisticRegression(class_weight = 'balanced')
# Con l siguiente los resultados mejoran sustancialemnte
logreg = LogisticRegression()
modelo = Pipeline([('standardizar', scalar),
('log_reg', logreg)])
modelo.fit(X_train, y_train)
y_train_hat = modelo.predict(X_train)
y_train_hat_probs = modelo.predict_proba(X_train)[:,1]
train_accuracidad = accuracy_score(y_train, y_train_hat)*100
train_auc_roc = roc_auc_score(y_train, y_train_hat_probs)*100
print('Confusion matrix:\n', confusion_matrix(y_train, y_train_hat))
print('Training AUC: %.4f %%' % train_auc_roc)
print('Training accuracy: %.4f %%' % train_accuracidad)
y_test_hat = modelo.predict(X_test)
y_test_hat_probs = modelo.predict_proba(X_test)[:,1]
test_accuracidad = accuracy_score(y_test, y_test_hat)*100
test_auc_roc = roc_auc_score(y_test, y_test_hat_probs)*100
print('Confusion matrix:\n', confusion_matrix(y_test, y_test_hat))
print('Testing AUC: %.4f %%' % test_auc_roc)
print('Testing accuracy: %.4f %%' % test_accuracidad)
print(classification_report(y_test, y_test_hat, digits=6))
3.3. Otro ejemplo de regresión logística#
#import pandas
import pandas as pd
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
# load dataset
pima = pd.read_csv("diabetes.csv", names=col_names)
pima = pima[1:]
pima.head()
| pregnant | glucose | bp | skin | insulin | bmi | pedigree | age | label | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 148 | 72 | 35 | 0 | 33.6 | 0.627 | 50 | 1 |
| 2 | 1 | 85 | 66 | 29 | 0 | 26.6 | 0.351 | 31 | 0 |
| 3 | 8 | 183 | 64 | 0 | 0 | 23.3 | 0.672 | 32 | 1 |
| 4 | 1 | 89 | 66 | 23 | 94 | 28.1 | 0.167 | 21 | 0 |
| 5 | 0 | 137 | 40 | 35 | 168 | 43.1 | 2.288 | 33 | 1 |
Selecting Feature
Here, you need to divide the given columns into two types of variables dependent(or target variable) and independent variable(or feature variables).
#split dataset in features and target variable
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variable
pima.dtypes
pregnant object
glucose object
bp object
skin object
insulin object
bmi object
pedigree object
age object
label object
dtype: object
# split X and y into training and testing sets
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=0)
# import the class
from sklearn.linear_model import LogisticRegression
# instantiate the model (using the default parameters)
logreg = LogisticRegression(solver='liblinear')
# fit the model with data
logreg.fit(X_train,y_train)
#
y_pred=logreg.predict(X_test)
# import the metrics class
from sklearn import metrics
cnf_matrix = metrics.confusion_matrix(y_test, y_pred)
cnf_matrix
array([[119, 11],
[ 26, 36]], dtype=int64)
3.4. Visualizar la matriz de confusión#
# import required modules
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
class_names=[0,1] # name of classes
fig, ax = plt.subplots()
tick_marks = np.arange(len(class_names))
plt.xticks(tick_marks, class_names)
plt.yticks(tick_marks, class_names)
# create heatmap
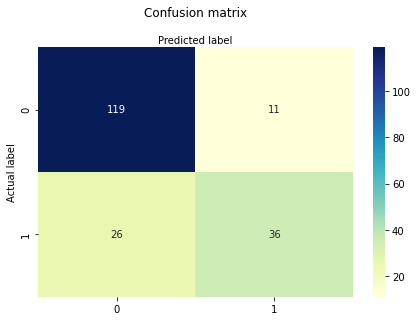
sns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')
ax.xaxis.set_label_position("top")
plt.tight_layout()
plt.title('Confusion matrix', y=1.1)
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
#Text(0.5,257.44,'Predicted label')
Text(0.5, 257.44, 'Predicted label')
3.5. diferentes métricas de la matriz de confusión#
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
print("Precision:",metrics.precision_score(y_test, y_pred, average=None))
print("Recall:",metrics.recall_score(y_test, y_pred, average = None))
Accuracy: 0.8072916666666666
Precision: [0.82068966 0.76595745]
Recall: [0.91538462 0.58064516]
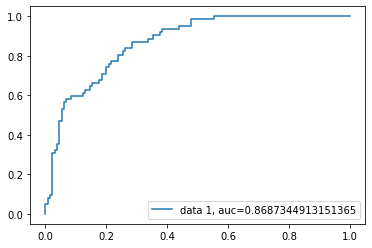
# Curva de ROC
y_pred_proba = logreg.predict_proba(X_test)[::,1]
fpr, tpr, _ = metrics.roc_curve(y_test.astype(int), y_pred_proba)
auc = metrics.roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()