Regresión con Python
Contenido
- Introducción
- Diferentes técnicas de pre-procesamiento
- Normalización de los datos
- Escalando los datos
- Normalization
- Binarizacion
- One Hot Encoding
- Codificación de etiquetas
- Ejemplo de regresión lineal
- Particiones Train Test
- Acuracidad del modelo
- Guardando el modelo obtenido
- regresión de tipo ridge
- Realizando una regresión polinómica
- Estimación precios de las casas
- Cálculo de la importancia relativa de las features
- Estimación de la demanda de bicicletas
Introducción
En el presente post, se van a presentar diferentes técnicas que se utilizan dentro del campo de machine learning para inferir valores a partir de una serie de datos observados. Son técnicas conocidas por la expresión supervised machine learning, dentro de las cuales por ejemplo se encuentra la regresión lineal, que más adelante se expondrá.
Antes de seguir hacia adelante con este tipo de técnicas, se van a presentar algunas herramientas que facilitan el tratamiento de la información antes de su procesamiento con este tipo de técnicas de análisis multivariante.
Diferentes técnicas de pre-procesamiento
En el tratamiento de datos, la información que llega en bruto adolece de muchos defectos tanto de forma como de contenido, que es preciso depurar y limpiar antes de que se proceda a su procesamiento con algún tipo de método estadístico.
Dentro de este procesamiento se pueden encontrar técnicas de imputación de valores faltantes, recodificación de variables, normalización de variables, etc. En los apartados que siguen, se va a proceder a exponer, sin ánimo de exhaustividad, algunos métodos que permiten realizar estas tareas.
import numpy as np
from sklearn import preprocessing
En el código anterior se ha importado el paquete scikit learn que permite realizar muchas operaciones utilizadas en machine learning. A continuación se genera una serie de datos, que nos servirán para exponer estas cuestiones más adelante.
data = np.array([[3, -1.5, 2, -5.4], [0, 4, -0.3, 2.1], [1, 3.3, -1.9, -4.3]])
print(data)
[[ 3. -1.5 2. -5.4]
[ 0. 4. -0.3 2.1]
[ 1. 3.3 -1.9 -4.3]]
Normalización de los datos
Con la finalidad de que todas las variables utilizadas en el procesamiento de la información tengan una escala de valores similar, lo que se suele hacer es normalizar esos datos, es decir, hacer una transformación de los mismos, para que tengan una media de cero y desviación típica 1. Para conseguir esto los que se hace es para columna restar la media muestral y dividirlo por la desviación típica de dicha muestra. Scikit learn tiene el método scale que nos permite hacer esto.
#Veamos el significado de axis=0 o axis=1
a=np.array([[1,1],[2,3]])
print(a)
print("\nMedia por columnas: ",a.mean(axis=0) )
print("\nMedia por filas: ",a.mean(axis=1))
#Luego axis=0 indica por columnas y axis=1 por filas
[[1 1]
[2 3]]
Media por columnas: [1.5 2. ]
Media por filas: [1. 2.5]
data_standardized = preprocessing.scale(data)
print(data_standardized)
### axis=0 indica columnas
print ("\Media =", data_standardized.mean(axis=0))
print ("Desviación típica =", data_standardized.std(axis=0))
[[ 1.33630621 -1.40451644 1.29110641 -0.86687558]
[-1.06904497 0.84543708 -0.14577008 1.40111286]
[-0.26726124 0.55907936 -1.14533633 -0.53423728]]
\Media = [ 5.55111512e-17 -1.11022302e-16 -7.40148683e-17 -7.40148683e-17]
Desviación típica = [1. 1. 1. 1.]
Como puede verse la media de cada columna es cero y la varianza es 1.
Escalando los datos
En otras ocasiones, lo que interesa es obtener valores dentro de un determinado rango, y para ello lo que se hace es escalar los datos para que todos queden dentro de ese rango pero manteniendo la proporción entre ellos. En el siguiente ejemplo, vamos a hacer esto para que los datos del ejemplo anterior se escalen y queden comprendidos entre los valores [0,1].
data_scaler = preprocessing.MinMaxScaler(feature_range=(0, 1))
data_scaled = data_scaler.fit_transform(data)
print ("\nMin max scaled data =\n", data_scaled)
Min max scaled data =
[[1. 0. 1. 0. ]
[0. 1. 0.41025641 1. ]
[0.33333333 0.87272727 0. 0.14666667]]
Normalization
Cuando se quiere trabajar con valores estandarizados pero con una determinada norma ( no tiene que ser necesariamente la euclídea), se utiliza este procedimiento para ello. En el ejemplo que sigue, se normalizan los valores utilizando la norma L1.
data_normalized = preprocessing.normalize(data, norm='l1')
print ("\nDatos normalizados por la norma L1=\n", data_normalized)
Datos normalizados por la norma L1=
[[ 0.25210084 -0.12605042 0.16806723 -0.45378151]
[ 0. 0.625 -0.046875 0.328125 ]
[ 0.0952381 0.31428571 -0.18095238 -0.40952381]]
Binarizacion
La binarización se utiliza para convertir variables continuas o discretas en otras variables de tipo boolean, es decir tomando sólo valores cero ó uno. Para conseguir esto hay que definir un determinado valor de corte, que en el ejemplo que sigue sería 1.4.
data_binarized = preprocessing.Binarizer(threshold=1.4).transform(data)
print ("\nDatos Binarizados =\n", data_binarized)
Datos Binarizados =
[[1. 0. 1. 0.]
[0. 1. 0. 1.]
[0. 1. 0. 0.]]
One Hot Encoding
Este procedimiento es el que en el mundo de la estadística también se denomina obtener variables de tipo dummy. Para hacer esto, se necesita una variable categórica, entonces esta variable va a dar origen a otra variables de tipo boolean (sólo tienen 1 y ceros), tantas como categorías tiene la categórica, de tal manera que un valor de categórica es equivalente a poner cero en todas las nuevas variables obtenidas, salvo aquella que representa la categoría del valor que toma la variable.
Pongamos un ejemplo que clarifique este concepto. Supongamos una variable categórica denominada “var” que puede tomar tres valores. Entonces al utilizar este procedimiento, se generarán otras tres variables que vamos a denominar “var_1,var_2 y var_3”. Si var toma el valor 1 entonces en la variables generadas, se obtendrían estos valores: 1,0,0. Si el valor tomado por var es el correspondiente a la segunda categoría, entonces los valores generados serían: 0,1,0 y por último si el valor es el de la tercera categoría, entonces el nuevo valor en las tres nuevas variables sería 0,0,1.
A continuación se muestra ejemplo práctico clarificador de todo lo comentado anteriormente.
Después de ejecutado el código que sigue, veamos cómo funciona esta función: la primera columna es 0, 1, 2, 1 es como si fuera una variable categórica con posibles valores 0,1,2.
Si tomamos el primer vector que se quiere codificar, es decir [2,3,5,3] el valor de la primera variable es 2, por lo tanto si generamos la variable “dummy” correspondiente sería [0,0,1].
Para el caso de las segunda variable, los valores posibles son 2 y 3, entones el valor 3 ( segundo elementos del vector que estamos codificando ) transformado a variable “dummy” seria [0,1].
Para la tercera variable los posibles valores de la variable categórica son: 1,2,4,5 por lo tanto 5 expresado como variable “dummy” sería [0,0,0,1].
Igual se haría con la cuarta variable, y al final de juntan todos los valores de las variables dummy’s obtenidas y se tiene el resultado que se aprecia en la salida del código ejecutado.
encoder = preprocessing.OneHotEncoder()
a=np.array([[0, 2, 1, 12], [1, 3, 5, 3], [2, 3, 2, 12], [1, 2, 4, 3]])
print(a)
encoder.fit(a)
encoded_vector = encoder.transform([[2, 3, 5, 3]]).toarray()
print ("\nVector codificado=", encoded_vector)
encoded_vector = encoder.transform([[2, 3, 5, 12]]).toarray()
print ("\nVector codificado=", encoded_vector)
encoded_vector=encoder.transform([[2, 3, 5, 3],[2, 3, 5, 12]])
#Obtenemos una sparse matrix (ver https://docs.scipy.org/doc/scipy/reference/sparse.html)
#cuyo significado es el siguiente: (0,9) 1.0 es que el elemento en (0,9) valie 1
#el elemento (0,8) vale 1, y así sucesivamente.
print("\nVector completo codificado(sparse matriz):\n",encoded_vector)
print("\nPonemos la matriz en formato dense\n")
print(encoded_vector.toarray())
#Lo siguiente nos da un error porque 24 no sabe cómo codificarlo
encoded_vector2 = encoder.transform([[24, 3, 5, 3]]).toarray()
print ("\vector2 codificado =", encoded_vector2)
[[ 0 2 1 12]
[ 1 3 5 3]
[ 2 3 2 12]
[ 1 2 4 3]]
Vector codificado= [[0. 0. 1. 0. 1. 0. 0. 0. 1. 1. 0.]]
Vector codificado= [[0. 0. 1. 0. 1. 0. 0. 0. 1. 0. 1.]]
Vector completo codificado(sparse matriz):
(0, 9) 1.0
(0, 8) 1.0
(0, 4) 1.0
(0, 2) 1.0
(1, 10) 1.0
(1, 8) 1.0
(1, 4) 1.0
(1, 2) 1.0
Ponemos la matriz en formato dense
[[0. 0. 1. 0. 1. 0. 0. 0. 1. 1. 0.]
[0. 0. 1. 0. 1. 0. 0. 0. 1. 0. 1.]]
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-94-5a9bdb90c339> in <module>()
19
20 #Lo siguiente nos da un error porque 24 no sabe cómo codificarlo
---> 21 encoded_vector2 = encoder.transform([[24, 3, 5, 3]]).toarray()
22 print ("\vector2 codificado =", encoded_vector2)
D:\programas\Anaconda\lib\site-packages\sklearn\preprocessing\data.py in transform(self, X)
2073 """
2074 return _transform_selected(X, self._transform,
-> 2075 self.categorical_features, copy=True)
2076
2077
D:\programas\Anaconda\lib\site-packages\sklearn\preprocessing\data.py in _transform_selected(X, transform, selected, copy)
1810
1811 if isinstance(selected, six.string_types) and selected == "all":
-> 1812 return transform(X)
1813
1814 if len(selected) == 0:
D:\programas\Anaconda\lib\site-packages\sklearn\preprocessing\data.py in _transform(self, X)
2044 if self.handle_unknown == 'error':
2045 raise ValueError("unknown categorical feature present %s "
-> 2046 "during transform." % X.ravel()[~mask])
2047
2048 column_indices = (X + indices[:-1]).ravel()[mask]
ValueError: unknown categorical feature present [24] during transform.
Codificación de etiquetas
Otra de las situaciones que se encuentran en el campo de machine learning es que ciertas variables categórica venga codificados con los caracteres, por ejemplo, la variable “sexo” puede venir codificada con los caracteres “varon”, “mujer”. Este tipo de codificación no permite el tratamiento con las utilidades que proporciona scikit learn. Por ello se deben pasar a valores numéricos, de esta manera por ejemplo “varon” pasará a valer 1 y “mujer” pasaría a valer 2.
Una vez pasados a valores numéricos, se podrían utilizar los métodos descritos en el apartado anterior (“One hot encoding”) y pasarlas a variables de tipo dummy. Veamos a continuación un ejemplo sobe cómo poder codificar con valores numéricos las categorías de tipo carácter de una variable categórica.
from sklearn import preprocessing
label_encoder = preprocessing.LabelEncoder()
input_classes = ['audi', 'ford', 'audi', 'toyota', 'ford', 'bmw']
label_encoder.fit(input_classes)
print ("\nMapeo de las clases:")
for i, item in enumerate(label_encoder.classes_):
print (item, '-->', i)
Mapeo de las clases:
audi --> 0
bmw --> 1
ford --> 2
toyota --> 3
Para codificar nuevos valores de la variable, se haría de la siguiente manera:
labels = ['toyota', 'ford', 'audi']
encoded_labels = label_encoder.transform(labels)
print ("\nEtiquetas =", labels)
print ("Etiquetas codificadas =", list(encoded_labels))
Etiquetas = ['toyota', 'ford', 'audi']
Etiquetas codificadas = [3, 2, 0]
El camino recíproco también se puede implementar. Es decir de una serie de valores numéricos, sacar las etiquetas con las que se corresponden.
encoded_labels = [2, 1, 0, 3, 1]
decoded_labels = label_encoder.inverse_transform(encoded_labels)
print ("\nEtiquetas codificadas =", encoded_labels)
print ("Etiquetas decodificadas =", list(decoded_labels))
Etiquetas codificadas = [2, 1, 0, 3, 1]
Etiquetas decodificadas = ['ford', 'bmw', 'audi', 'toyota', 'bmw']
D:\programas\Anaconda\lib\site-packages\sklearn\preprocessing\label.py:151: DeprecationWarning: The truth value of an empty array is ambiguous. Returning False, but in future this will result in an error. Use `array.size > 0` to check that an array is not empty.
if diff:
Ejemplo de regresión lineal
Estas técnicas de regresión se denominan como mínimos cuadrados ordinarios, ya que lo que buscan es minimizar la suma de las distancias al cuadrado entre el punto y el valor predicho. En Python este tipo de técnicas se realizan utilizando el módulo LinearRegression de scikit Learn.
En consecuencia si X es la matriz de los datos de lo que se trata es de hacer una estimación de la forma: \( y=Xw+\epsilon \) de tal manera que se optimize
\[ \underset{w}{min}{\parallel Xw-y \parallel _{2}} ^{2} \]
Para realizar este trabajo, vamos a utilizar un fichero denominado data_singlevar.txt que contiene en cada linea dos campos de datos separados por una coma. El fichero con el que se va a trabajar, se puede encontrar en Github en la dirección que figura en el siguiente código.
import pandas as pd
#url='https://github.com/PacktPublishing/Python-Machine-Learning-Cookbook/blob/master/Chapter01/data_singlevar.txt'
url='https://raw.githubusercontent.com/PacktPublishing/Python-Machine-Learning-Cookbook/master/Chapter01/data_singlevar.txt'
a=pd.read_csv(url,header=None)
print(a.head(6))
X=a.iloc[:,0]
y=a.iloc[:,1]
print(type(X))
print(X.to_frame().T )
print(y.to_frame().T)
0 1
0 4.94 4.37
1 -1.58 1.70
2 -4.45 1.88
3 -6.06 0.56
4 -1.22 2.23
5 -3.55 1.53
<class 'pandas.core.series.Series'>
0 1 2 3 4 5 6 7 8 9 ... 40 \
0 4.94 -1.58 -4.45 -6.06 -1.22 -3.55 0.36 -3.24 1.31 2.17 ... -1.81
41 42 43 44 45 46 47 48 49
0 3.94 -2.0 0.54 0.78 2.15 2.55 -0.63 1.06 -0.36
[1 rows x 50 columns]
0 1 2 3 4 5 6 7 8 9 ... 40 \
1 4.37 1.7 1.88 0.56 2.23 1.53 2.99 0.48 2.76 3.99 ... 2.85
41 42 43 44 45 46 47 48 49
1 4.86 1.31 3.99 2.92 4.72 3.83 2.58 2.89 1.99
[1 rows x 50 columns]
Particiones Train Test
Cuando se pretende construir un modelo que se ajuste a una serie de datos, es conveniente probar el ajuste que se ha obtenido. Para ello existen diversos procedimientos, pero uno de los más utilizados consiste en el de entrenamiento-test. En estos casos, se dividen los datos en dos conjuntos: uno es el que servirá para entrenar el modelo, y el otro conjunto servirá para testear los resultados obtenidos ( los dos conjuntos se suelen llamar train-test).
Scikit learm presenta tiene una función denominada sklearn.model_selection.train_test_split{:target=’_blank’), que sirve para realizar este tipo de procesos. Sin embargo a efectos meramente ilustrativos a continuación se muestra un procedimiento para conseguir este objetivo. Con este procedimiento se selecciona el 80 por ciento de los datos con train y el resto serán de tipo test.
num_training = int(0.8 * len(X))
num_test = len(X) - num_training
# Training data
X_train = np.array(X[:num_training]).reshape((num_training,1))
y_train = np.array(y[:num_training])
# Test data
X_test = np.array(X[num_training:]).reshape((num_test,1))
y_test = np.array(y[num_training:])
A continuación lo que se hace es construir el modelo:
from sklearn import linear_model
# Crea un objeto de tipo regresión lineal
linear_regressor = linear_model.LinearRegression()
# Se ajusta el modelo con la parte train que se ha obtenido antes
linear_regressor.fit(X_train, y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
Ahora hacemos una representación gráfica de los datos iniciales y la recta de regresión que hemos obtenido
import matplotlib.pyplot as plt
y_train_pred = linear_regressor.predict(X_train)
plt.figure()
plt.scatter(X_train, y_train, color='green')
plt.plot(X_train, y_train_pred, color='black', linewidth=4)
plt.title('Training data')
plt.show()
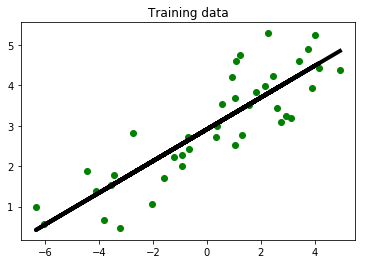
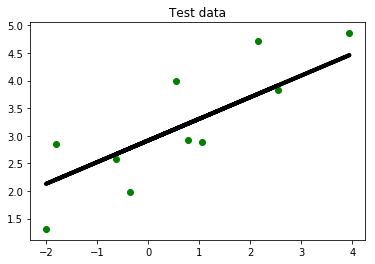
A continuación tomamos los datos de la parte de test’s y calculamos los valores predichos, para compararlos con los valores reales.
y_test_pred = linear_regressor.predict(X_test)
plt.scatter(X_test, y_test, color='green')
plt.plot(X_test, y_test_pred, color='black', linewidth=4)
plt.title('Test data')
plt.show()
Acuracidad del modelo
Existen una serie de indicadores que sirven para estudiar y evaluar cuando se alejan los datos previstos de los reales. Los indicadores más importante son los siguientes:
- Mean absolute error: Es un promedio de los errores absolutos que hay entre los datos reales y los previstos por el modelo.
- Mean squared error: Es una media de los errores al cuadrado.
- Median absolute error: Lo mismo que para la media, pero calculando la mediana de los errores absolutos
- Explained variance score: Mide la variación explicada por el modelo. Cuanto más cercano a 1 mejor.
- R2 score: También se denomina R-squared, o también coeficiente de determinación. Mide la cantidad de variabilidad que el modelo explica. Cuanto más cerca de 1 se encuentre mejor explicación se tendrá del modelo..
import sklearn.metrics as sm
print("Error absoluto medio =", round(sm.mean_absolute_error(y_test, y_test_pred), 2))
print("MSE ó Mean squared error =", round(sm.mean_squared_error(y_test, y_test_pred), 2))
print ("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2))
print ("Explained variance score =", round(sm.explained_variance_score(y_test, y_test_pred), 2))
print ("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))
Error absoluto medio = 0.54
MSE ó Mean squared error = 0.38
Median absolute error = 0.54
Explained variance score = 0.68
R2 score = 0.68
Guardando el modelo obtenido
Una vez obtenido un modelo, con la finalidad de no tener que ejcutar pasos anteriores ya hechos y que en ocasiones pueden ser bastante lentos, conviene guardar en disco duro el modelo obtenido, para después poder recuperarlo y trabajar de forma rápida con él.
import pickle
#Esto se ha hecho en Python 3, en Python 2 hay importar cPickle
s = pickle.dumps(linear_regressor)
#Para Python 2 el código sería el siguiente
#output_model_file = 'saved_model.pkl'
#with open(output_model_file, 'w') as f:
# pickle.dump(linear_regressor, f)
El objeto se ha guardado y se mantendrá guardado aunque el ordenador de trabajo se haya apagado. Posteriormente se podrá recuperar de la siguiente manera.
#with open(output_model_file, 'r') as f:
# model_linregr = pickle.load(f)
#y_test_pred_new = model_linregr.predict(X_test)
#print "\nNew mean absolute error =", round(sm.mean_absolute_error(y_test, y_test_pred_new), 2)
#Ahora se recupera de la siguiente manera
s2 = pickle.loads(s)
print(s2.predict(X_test))
print("Anteriormente los datos previstos fueron: \n",y_test_pred)
[2.20369892 4.45873314 2.12918475 3.1253216 3.21944477 3.75673118
3.91360313 2.66647116 3.32925513 2.77235973]
Anteriormente los datos previstos fueron:
[2.20369892 4.45873314 2.12918475 3.1253216 3.21944477 3.75673118
3.91360313 2.66647116 3.32925513 2.77235973]
regresión de tipo ridge
Con la regresión ridge lo que se trata es “perturbar” ligeramente la matriz X′X para que deje de ser aproximadamente singular. En este caso lo que se hace es resolver
\[ \underset{w}{min}{\parallel Xw-y \parallel _{2}} ^{2} +\alpha{\parallel X \parallel _{2}} ^{2} \]
ridge_regressor = linear_model.Ridge(alpha=0.01, fit_intercept=True, max_iter=10000)
Obtenemos además los siguientes índices:
ridge_regressor.fit(X_train, y_train)
y_test_pred_ridge = ridge_regressor.predict(X_test)
print ("Mean absolute error =", round(sm.mean_absolute_error(y_test, y_test_pred_ridge), 2) )
print ("Mean squared error =", round(sm.mean_squared_error(y_test, y_test_pred_ridge), 2) )
print ("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred_ridge), 2) )
print ("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred_ridge), 2) )
print ("R2 score =", round(sm.r2_score(y_test, y_test_pred_ridge), 2))
Mean absolute error = 0.54
Mean squared error = 0.38
Median absolute error = 0.54
Explain variance score = 0.68
R2 score = 0.68
Realizando una regresión polinómica
El ajuste se puede hacer también utilizando una función de tipo polinómica. En este caso se muestra un ejemplo de ajuste polinómico de grado 3.
from sklearn.preprocessing import PolynomialFeatures
polynomial = PolynomialFeatures(degree=3)
Los valores obtenidos mediante el ajuste anterior, se obtienen de la siguiente manera:
X_train_transformed = polynomial.fit_transform(X_train)
A continuación se muestra la diferencia que hay a la hora de predecir un punto bajo diferentes modelos
datapoint = [[0.39],[2.78],[7.11]]
poly_datapoint = polynomial.fit_transform(datapoint)
poly_linear_model = linear_model.LinearRegression()
poly_linear_model.fit(X_train_transformed, y_train)
print( "\nLinear regression:", linear_regressor.predict(datapoint)[0])
print ("\nPolynomial regression:", poly_linear_model.predict(poly_datapoint)[0])
Linear regression: 3.0664946237330555
Polynomial regression: 3.1136002107457923
Estimación precios de las casas
En este caso no tenemos una sola variable regresor, si no que tenemos muchas más, como se muestra en poco más abajo, y de lo que se trata es estimar el precio de las viviendas, en base al resto de regresores.
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import AdaBoostRegressor
from sklearn import datasets
from sklearn.metrics import mean_squared_error, explained_variance_score
from sklearn.utils import shuffle
import matplotlib.pyplot as plt
housing_data = datasets.load_boston()
print(type(housing_data.data))
print(housing_data.data[0:5])
print("Los nombre de las variables son:")
print(housing_data.feature_names)
<class 'numpy.ndarray'>
[[6.3200e-03 1.8000e+01 2.3100e+00 0.0000e+00 5.3800e-01 6.5750e+00
6.5200e+01 4.0900e+00 1.0000e+00 2.9600e+02 1.5300e+01 3.9690e+02
4.9800e+00]
[2.7310e-02 0.0000e+00 7.0700e+00 0.0000e+00 4.6900e-01 6.4210e+00
7.8900e+01 4.9671e+00 2.0000e+00 2.4200e+02 1.7800e+01 3.9690e+02
9.1400e+00]
[2.7290e-02 0.0000e+00 7.0700e+00 0.0000e+00 4.6900e-01 7.1850e+00
6.1100e+01 4.9671e+00 2.0000e+00 2.4200e+02 1.7800e+01 3.9283e+02
4.0300e+00]
[3.2370e-02 0.0000e+00 2.1800e+00 0.0000e+00 4.5800e-01 6.9980e+00
4.5800e+01 6.0622e+00 3.0000e+00 2.2200e+02 1.8700e+01 3.9463e+02
2.9400e+00]
[6.9050e-02 0.0000e+00 2.1800e+00 0.0000e+00 4.5800e-01 7.1470e+00
5.4200e+01 6.0622e+00 3.0000e+00 2.2200e+02 1.8700e+01 3.9690e+02
5.3300e+00]]
Los nombre de las variables son:
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
'B' 'LSTAT']
Lo primero que hacemos es una reordenación aleatoria de los datos con los que se va a trabajar.
X, y = shuffle(housing_data.data, housing_data.target, random_state=7)
Ahora seleccionamos el 80 por ciento de los datos como datos para el entrenamiento y el resto sirve para testear el modelo obtenido.
num_training = int(0.8 * len(X))
X_train, y_train = X[:num_training], y[:num_training]
X_test, y_test = X[num_training:], y[num_training:]
Ahora utilizamos un modelo de tipo “regressión tree” para el ajuste de nuestros datos.
dt_regressor = DecisionTreeRegressor(max_depth=4)
dt_regressor.fit(X_train, y_train)
DecisionTreeRegressor(criterion='mse', max_depth=4, max_features=None,
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best')
#Para obtener el R^2 de la predicción
dt_regressor.score(X_train,y_train)
0.8938416214458438
También utilizamos el modelo AdaBoost.Un regresor AdaBoost [1] es un metaestimador que comienza ajustando un regresor en el conjunto de datos original y luego ajusta copias adicionales del regresor en el mismo conjunto de datos, pero donde los pesos de las instancias se ajustan de acuerdo con el error de la predicción actual. Como tal, los regresores posteriores se enfocan más en casos difíciles.
ab_regressor = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=400, random_state=7)
ab_regressor.fit(X_train, y_train)
AdaBoostRegressor(base_estimator=DecisionTreeRegressor(criterion='mse', max_depth=4, max_features=None,
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best'),
learning_rate=1.0, loss='linear', n_estimators=400,
random_state=7)
Veamos como AdaBoost mejora los ajustes del modelo
y_pred_dt = dt_regressor.predict(X_test)
mse = mean_squared_error(y_test, y_pred_dt)
evs = explained_variance_score(y_test, y_pred_dt)
print ("\n#### Decision Tree performance ####")
print ("Mean squared error =", round(mse, 2))
print ("Explained variance score =", round(evs, 2))
#### Decision Tree performance ####
Mean squared error = 14.79
Explained variance score = 0.82
Ahora hacemos la evaluación con AdaBoost:
y_pred_ab = ab_regressor.predict(X_test)
mse = mean_squared_error(y_test, y_pred_ab)
evs = explained_variance_score(y_test, y_pred_ab)
print ("\n#### AdaBoost performance ####")
print ("Mean squared error =", round(mse, 2))
print ("Explained variance score =", round(evs, 2))
#### AdaBoost performance ####
Mean squared error = 7.64
Explained variance score = 0.91
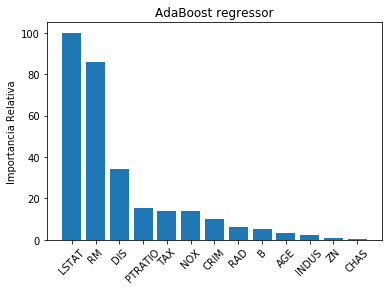
El error es menor y la variance score más cerca de 1 si se utliza AdaBoost, por lo tanto el ajuste mejora con este modelo.
Cálculo de la importancia relativa de las features
Con la siguiente función lo que se hace es calcular la importancia relativa de cada una de las 13 features utilizadas para hacer la regresión.
def plot_feature_importances(feature_importances, title, feature_names):
# Normalize the importance values
feature_importances = 100.0 * (feature_importances / max(feature_importances))
# Sort the index values and flip them so that they are arranged in decreasing order of importance
index_sorted = np.flipud(np.argsort(feature_importances))
# Center the location of the labels on the X-axis (for display purposes only)
pos = np.arange(index_sorted.shape[0]) + 0.5
# Plot the bar graph
plt.figure()
plt.bar(pos, feature_importances[index_sorted], align='center')
plt.xticks(pos, feature_names[index_sorted])
plt.ylabel('Importancia Relativa')
plt.title(title)
plt.xticks(rotation=45)
plt.show()
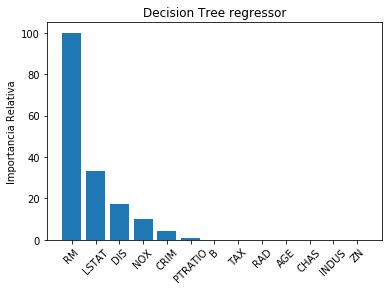
plot_feature_importances(dt_regressor.feature_importances_,
'Decision Tree regressor', housing_data.feature_names)
plot_feature_importances(ab_regressor.feature_importances_,
'AdaBoost regressor', housing_data.feature_names)
Estimación de la demanda de bicicletas
En este apartado vamos a utilizar otro método de regresión para estimar la demanda de bicicletas. Para ello se utiliza el método de “random forest regressor”, que se basa en calcular varios “decision trees” para después promediar los resultados.
Se va a usar un fichero de demandas de bicicletas, que se puede localizar en este enlace.
En este conjunto de datos hay un total de 16 columnas. Las dos primeras tienen número de serie y fecha, por lo que no las necesitamos para el análisis. La última columna es la suma de las dos anteriores (la decimocuarta y decimoquinta). Por lo tanto la decimocuarta y decimoquinta no se utilizarán en este ajuste.
Creamos inicialmente una función para leer los datos.
import csv
from sklearn.ensemble import RandomForestRegressor
#from housing import plot_feature_importances
def load_dataset(filename):
file_reader = csv.reader(open(filename, 'rt'), delimiter=',')
X, y = [], []
for row in file_reader:
X.append(row[2:13])
y.append(row[-1])
# Extract feature names
feature_names = np.array(X[0])
# Remove the first row because they are feature names
return np.array(X[1:]).astype(np.float32), np.array(y[1:]).astype(np.float32), feature_names
Ahora procedemos a la lectura de los datos y definimos también los nombre de las variables o features:
X, y, feature_names = load_dataset('F:/MisCodigos/web/data/day.csv')
X, y = shuffle(X, y, random_state=7)
print(feature_names)
['season' 'yr' 'mnth' 'holiday' 'weekday' 'workingday' 'weathersit' 'temp'
'atemp' 'hum' 'windspeed']
print(X[0:5])
[[ 4. 1. 12. 0. 0. 0.
2. 0.384167 0.390146 0.905417 0.157975 ]
[ 4. 1. 11. 0. 2. 1.
2. 0.291667 0.281558 0.786667 0.237562 ]
[ 3. 1. 9. 0. 0. 0.
1. 0.58 0.563125 0.57 0.0901833]
[ 4. 0. 11. 0. 2. 1.
1. 0.400833 0.397088 0.68375 0.135571 ]
[ 4. 0. 11. 0. 3. 1.
1. 0.325 0.311221 0.613333 0.271158 ]]
print(y[0:5])
[3228. 3959. 7333. 4068. 3613.]
Generamos ahora los conjuntos train y test
num_training = int(0.9 * len(X))
X_train, y_train = X[:num_training], y[:num_training]
X_test, y_test = X[num_training:], y[num_training:]
Y ahora generamos el modelo:
rf_regressor = RandomForestRegressor(n_estimators=1000, max_depth=10, min_samples_split=2)
rf_regressor.fit(X_train, y_train)
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=10,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=1000, n_jobs=1,
oob_score=False, random_state=None, verbose=0, warm_start=False)
Respecto a los parámetros utilizados cabe decir que n_estimators se refiere al número de estimadores calculados que además coincide con el número de modelos de decision tree que se va a utilizar. El parámetro max_depth se refiere a la máxima profundidad de cada decision tree y por último min_samples_split se refiere a la cantidad de muestras de datos que se necesitan para dividir un nodo en el árbol.
A continuación evaluamos la calidad del modelo:
y_pred = rf_regressor.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
evs = explained_variance_score(y_test, y_pred)
print ("\n#### Random Forest regressor performance ####")
print ("Mean squared error =", round(mse, 2))
print ("Explained variance score =", round(evs, 2))
#### Random Forest regressor performance ####
Mean squared error = 363675.87
Explained variance score = 0.89
Y ahora calculamos y representamos la importancia de cada feature.
plot_feature_importances(rf_regressor.feature_importances_, 'Random Forest regressor', feature_names)
