Regresión Logit (Stepwise)
Contenido
- Introducción
- Presentación de los datos
- Modelo paso a paso forward
- Método forward
- Método backward
- Utilización de Leave-One-Out Cross Validación
Introducción
En un post anterior ya se ha expuesto que se puede utilizar el criterio marcado por el indicador “IV” para seleccionar las variables que entrarían en el análisis. En el presente post, se va a utilizar otro criterio para hacer una selección de las variables a utilizar.
En este caso utilizaremos el método paso a paso ( stepwise, en terminología anglosajona ), que consiste en ir probando modelos hasta quedarnos con el que mejor explique el sistema que se está estudiando.
En este caso existen dos métodos generales, que son los siguientes:
1.- forward. Es decir “hacia adelante”, que consiste en elegir un modelo básico y después ir añadiendo variables y mirando cómo va mejorando la capacidad explicativa del modelo, hasta llegar a un punto en que dicha capacidad explicativa no compensa la introducción de nuevas variables.
2.- backward. Es decir “hacia atrás”, que sería el recíproco del caso anterior, es decir partimos de un modelo con muchas variables y vamos eliminado hasta la disminución en la capacidad explicativa del modelo sea significativa.
Igualmente en este post también se va a exponer otro método de selección de variables basado en un método denominado “Leave-One-Out Cross Validación”, inspirado en el método de validación de machine learning que lleva el mismo nombre.
Presentación de los datos
Vamos a ver cómo utilizar este método de selección de variables.
datos=read.table(
"http://freakonometrics.free.fr/saporta.csv",
head=TRUE,sep=";")
head(datos)
## FRCAR INCAR INSYS PRDIA PAPUL PVENT REPUL PRONO
## 1 90 1.71 19.0 16 19.5 16.0 912 SURVIE
## 2 90 1.68 18.7 24 31.0 14.0 1476 DECES
## 3 120 1.40 11.7 23 29.0 8.0 1657 DECES
## 4 82 1.79 21.8 14 17.5 10.0 782 SURVIE
## 5 80 1.58 19.7 21 28.0 18.5 1418 DECES
## 6 80 1.13 14.1 18 23.5 9.0 1664 DECES
Las observaciones se corresponden a personas que ingresan en urgencias debido a un (posible) infarto, queremos modelar estos datos para construir un modelo predictivo.
str(datos)
## 'data.frame': 71 obs. of 8 variables:
## $ FRCAR: int 90 90 120 82 80 80 94 80 78 100 ...
## $ INCAR: num 1.71 1.68 1.4 1.79 1.58 1.13 2.04 1.19 2.16 2.28 ...
## $ INSYS: num 19 18.7 11.7 21.8 19.7 14.1 21.7 14.9 27.7 22.8 ...
## $ PRDIA: int 16 24 23 14 21 18 23 16 15 16 ...
## $ PAPUL: num 19.5 31 29 17.5 28 23.5 27 21 20.5 23 ...
## $ PVENT: num 16 14 8 10 18.5 9 10 16.5 11.5 4 ...
## $ REPUL: int 912 1476 1657 782 1418 1664 1059 1412 759 807 ...
## $ PRONO: Factor w/ 2 levels "DECES","SURVIE": 2 1 1 2 1 1 2 2 2 2 ...
A continuación vamos a ver´cómo poder construir un modelo paso a paso. Utilizaremos para este caso el criterio de información de Akaike.
El criterio de información (AIC) de Akaike, se obtiene de la siguiente manera:
\[ AIC=2k-2ln(\widehat{L}) \]
Donde k es el número de parámetros estimados en el modelo y \( \widehat{L} \) es el máximo de la función de verosimilitud.
Modelo paso a paso forward
Se construye inicialmente el modelo más corto y el modelo completo, para después ir poco a poco añadiendo variables
reg0=glm(PRONO~1,data=datos,family=binomial)
summary(reg0)
##
## Call:
## glm(formula = PRONO ~ 1, family = binomial, data = datos)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.338 -1.338 1.025 1.025 1.025
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.3704 0.2414 1.534 0.125
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 96.033 on 70 degrees of freedom
## Residual deviance: 96.033 on 70 degrees of freedom
## AIC: 98.033
##
## Number of Fisher Scoring iterations: 4
reg1=glm(PRONO~.,data=datos,family=binomial)
summary(reg1)
##
## Call:
## glm(formula = PRONO ~ ., family = binomial, data = datos)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.24911 -0.41613 0.05261 0.39611 2.25781
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -10.187642 11.895227 -0.856 0.392
## FRCAR 0.138178 0.114112 1.211 0.226
## INCAR -5.862429 6.748785 -0.869 0.385
## INSYS 0.717084 0.561445 1.277 0.202
## PRDIA -0.073668 0.291636 -0.253 0.801
## PAPUL 0.016757 0.341942 0.049 0.961
## PVENT -0.106776 0.110550 -0.966 0.334
## REPUL -0.003154 0.004891 -0.645 0.519
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 96.033 on 70 degrees of freedom
## Residual deviance: 41.043 on 63 degrees of freedom
## AIC: 57.043
##
## Number of Fisher Scoring iterations: 7
Como vemos el valor del criterio de información de Akaike (AIC) disminuye del modelo más básico al completo. Veamos paso a paso cuando se para el proceso y con qué variables nos quedamos. Tener presente que se utiliza el parámetro “K=2” para utilizar el criterio AIC como elemento de parada del modelo.
Método forward
step(reg0,scope=formula(reg1),direction="forward",k=2)
## Start: AIC=98.03
## PRONO ~ 1
##
## Df Deviance AIC
## + REPUL 1 46.884 50.884
## + INSYS 1 51.865 55.865
## + INCAR 1 53.313 57.313
## + PRDIA 1 78.503 82.503
## + PAPUL 1 82.862 86.862
## + PVENT 1 87.093 91.093
## <none> 96.033 98.033
## + FRCAR 1 94.861 98.861
##
## Step: AIC=50.88
## PRONO ~ REPUL
##
## Df Deviance AIC
## + INCAR 1 44.530 50.530
## + PVENT 1 44.703 50.703
## + INSYS 1 44.857 50.857
## <none> 46.884 50.884
## + PAPUL 1 45.274 51.274
## + PRDIA 1 46.322 52.322
## + FRCAR 1 46.540 52.540
##
## Step: AIC=50.53
## PRONO ~ REPUL + INCAR
##
## Df Deviance AIC
## <none> 44.530 50.530
## + PVENT 1 43.134 51.134
## + PRDIA 1 43.772 51.772
## + INSYS 1 44.305 52.305
## + PAPUL 1 44.341 52.341
## + FRCAR 1 44.521 52.521
##
## Call: glm(formula = PRONO ~ REPUL + INCAR, family = binomial, data = datos)
##
## Coefficients:
## (Intercept) REPUL INCAR
## 1.633668 -0.003564 1.618479
##
## Degrees of Freedom: 70 Total (i.e. Null); 68 Residual
## Null Deviance: 96.03
## Residual Deviance: 44.53 AIC: 50.53
Observamos que se queda con dos variables: REPUL e INCAR y con eso ya tenemos un valor de AIC=50.53, muy cerca del valor AIC para el modelo completo.
Si utilizamos el criterio Schwarz Bayesian Information Criterion ( BIC ), se cambiaría respecto del modelo anterior que en este caso el valor del parámetro k sería k=log(n) siendo n el número de elementos de la muestra. Los resultados que se obtendrán serán los siguientes:
n=nrow(datos)
step(reg0,scope=formula(reg1),direction="forward",k=log(n))
## Start: AIC=100.3
## PRONO ~ 1
##
## Df Deviance AIC
## + REPUL 1 46.884 55.409
## + INSYS 1 51.865 60.390
## + INCAR 1 53.313 61.838
## + PRDIA 1 78.503 87.029
## + PAPUL 1 82.862 91.388
## + PVENT 1 87.093 95.618
## <none> 96.033 100.296
## + FRCAR 1 94.861 103.386
##
## Step: AIC=55.41
## PRONO ~ REPUL
##
## Df Deviance AIC
## <none> 46.884 55.409
## + INCAR 1 44.530 57.318
## + PVENT 1 44.703 57.492
## + INSYS 1 44.857 57.645
## + PAPUL 1 45.274 58.062
## + PRDIA 1 46.322 59.110
## + FRCAR 1 46.540 59.328
##
## Call: glm(formula = PRONO ~ REPUL, family = binomial, data = datos)
##
## Coefficients:
## (Intercept) REPUL
## 6.252328 -0.005011
##
## Degrees of Freedom: 70 Total (i.e. Null); 69 Residual
## Null Deviance: 96.03
## Residual Deviance: 46.88 AIC: 50.88
En consecuencia, con el código anterior se puede ver que la variable REPUL es la que de forma segura hay que añadir al análisis, y además se mejora el modelo, añadiendo la variable INCAR.
Hay que tener en cuenta que según Stone(1977), los resultados obtenidos con AIC son asintóticamente equivalentes a un One-Leave-Out Cross validatión, mientras que los datos obtenidos con BIC son asintóticamente equivalentes a los resultados obtenidos con un k-fold Cross Validation (Shao(1.997)), con
\[ k=n[1-1/(log(n)-1)] \]
Método backward
Veamos cómo sería si utilizamos el método backward ( es decir hacia atrás ). El código es muy similar al usado anteriormente y sería el siguiente.
step(reg1,scope=formula(reg0),direction="backward",k=2)
## Start: AIC=57.04
## PRONO ~ FRCAR + INCAR + INSYS + PRDIA + PAPUL + PVENT + REPUL
##
## Df Deviance AIC
## - PAPUL 1 41.046 55.046
## - PRDIA 1 41.107 55.107
## - REPUL 1 41.482 55.482
## - INCAR 1 41.776 55.776
## - PVENT 1 41.972 55.972
## - FRCAR 1 42.548 56.548
## - INSYS 1 42.879 56.879
## <none> 41.043 57.043
##
## Step: AIC=55.05
## PRONO ~ FRCAR + INCAR + INSYS + PRDIA + PVENT + REPUL
##
## Df Deviance AIC
## - PRDIA 1 41.158 53.158
## - INCAR 1 41.903 53.903
## - REPUL 1 42.062 54.062
## - PVENT 1 42.176 54.176
## - FRCAR 1 42.557 54.557
## - INSYS 1 42.885 54.885
## <none> 41.046 55.046
##
## Step: AIC=53.16
## PRONO ~ FRCAR + INCAR + INSYS + PVENT + REPUL
##
## Df Deviance AIC
## - INCAR 1 42.327 52.327
## - FRCAR 1 42.663 52.663
## - PVENT 1 42.810 52.810
## - INSYS 1 43.046 53.046
## <none> 41.158 53.158
## - REPUL 1 47.764 57.764
##
## Step: AIC=52.33
## PRONO ~ FRCAR + INSYS + PVENT + REPUL
##
## Df Deviance AIC
## - FRCAR 1 42.810 50.810
## - PVENT 1 43.786 51.786
## <none> 42.327 52.327
## - INSYS 1 44.636 52.636
## - REPUL 1 48.175 56.175
##
## Step: AIC=50.81
## PRONO ~ INSYS + PVENT + REPUL
##
## Df Deviance AIC
## - INSYS 1 44.703 50.703
## <none> 42.810 50.810
## - PVENT 1 44.857 50.857
## - REPUL 1 49.136 55.136
##
## Step: AIC=50.7
## PRONO ~ PVENT + REPUL
##
## Df Deviance AIC
## <none> 44.703 50.703
## - PVENT 1 46.884 50.884
## - REPUL 1 87.093 91.093
##
## Call: glm(formula = PRONO ~ PVENT + REPUL, family = binomial, data = datos)
##
## Coefficients:
## (Intercept) PVENT REPUL
## 7.536215 -0.122659 -0.004972
##
## Degrees of Freedom: 70 Total (i.e. Null); 68 Residual
## Null Deviance: 96.03
## Residual Deviance: 44.7 AIC: 50.7
Si no queremos que el método nos de mucha información se puede introducir el parámetro “trace=F”, tal y como hacemos en el siguiente código.
step(reg0,scope=formula(reg1),direction="forward",k=2, trace = F)
##
## Call: glm(formula = PRONO ~ REPUL + INCAR, family = binomial, data = datos)
##
## Coefficients:
## (Intercept) REPUL INCAR
## 1.633668 -0.003564 1.618479
##
## Degrees of Freedom: 70 Total (i.e. Null); 68 Residual
## Null Deviance: 96.03
## Residual Deviance: 44.53 AIC: 50.53
Utilización de Leave-One-Out Cross Validación
El método denominado Leave-One-Out Cross Validación es muy utilizado en machine learning para validar un modelo. En este caso este método consiste en los siguiente.
Crearemos 7 modelos de regresión logística, cada uno conteniendo como regresor una variable de la 7 variables independientes con las que se trabaja. Una vez definida una variable independiente y por lo tanto un modelo, generamos el modelo de regresión logit con n-1 observación y dejamos la restante para calcular la predicción que nos da el modelo. Si para cada modelo repetimos este proceso n veces, dejando en cada paso una observación diferente para predicción, al final lo que tenemos es un vector con n predicciones.
Veamos a continuación cómo implementar este procedimiento. En primer lugar definimos la función “pred_i” que para cada n-1 observaciones y una sola variable independiente crea un modelo de regresión logit y calcula la predicción para el valor de la observación que no ha entrado en la construcción del modelo.
name_var=names(datos) #Tomamos los nombres de las variables
pred_i=function(i,k){
#Definimos la fórmula de regresión (una para cada variable)
fml = paste(name_var[8],"~",name_var[k],sep="")
#Definimos y calculamos el modelo. -i==eliminar observación i
reg=glm(fml,data=datos[-i,],family=binomial)
#Generamos la predicción
predict(reg,newdata=datos[i,],type="response")
}
A continuación y apoyándonos en la función definida anteriormente, calculamos la curva de roc y su área correspondiente, para cada uno de los 7 modelos que se han construido y que están relacionados biunivocamente con las 7 variables independientes con las que trabajamos.
if (!require("AUC")) install.packages("AUC"); require("AUC")
## Loading required package: AUC
## AUC 0.3.0
## Type AUCNews() to see the change log and ?AUC to get an overview.
ROC=function(k){
# Lammamos Y a la variable dependiente, es la que ocupa lugar 8
Y=datos[,8]=="SURVIE"
#Metemos las predicciones en un vector
S=Vectorize(function(i) pred_i(i,k))(1:length(Y))
#Calculamos la curva de roc y el área
R=roc(S,as.factor(Y))
return(list(roc=cbind(R$fpr,R$tpr), auc=AUC::auc(R)))
}
Mostramos para cada una de las variables el valor del área que queda por debajo de la curva de roc del modelo correspondiente.
AUC=rep(NA,7)
for(k in 1:7){
AUC[k]=ROC(k)$auc
cat("Variable ",k,"(",name_var[k],") :",
AUC[k],"\n") }
## Variable 1 ( FRCAR ) : 0.4934319
## Variable 2 ( INCAR ) : 0.8965517
## Variable 3 ( INSYS ) : 0.909688
## Variable 4 ( PRDIA ) : 0.7487685
## Variable 5 ( PAPUL ) : 0.7134647
## Variable 6 ( PVENT ) : 0.6584565
## Variable 7 ( REPUL ) : 0.9154351
Vemos que el mejor valor se obtiene para la variable “REPUL” y será la primera variable independiente que entre en el modelo.
Veamos cómo quedarían las curvas de roc de cada uno de los 7 modelos generados.
if (!require("RColorBrewer")) install.packages("RColorBrewer"); require("RColorBrewer")
## Loading required package: RColorBrewer
CL=brewer.pal(8, "Set1")[-7]
plot(0:1,0:1,col="white",xlab="",ylab="")
for(k in 1:7)
lines(ROC(k)$roc,type="s",col=CL[k])
legend(.8,.55,name_var,col=CL,lty=1,cex=.8)
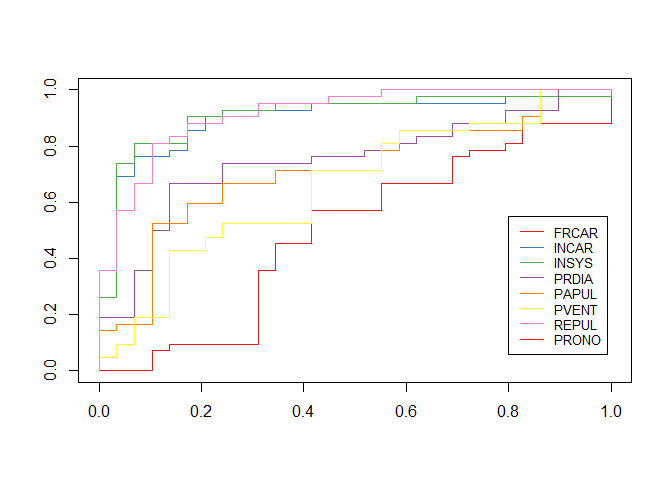
k0=which.max(AUC)
print( paste("Primera variable que entra en el análisis: ", name_var[k0]))
## [1] "Primera variable que entra en el análisis: REPUL"
Una vez obtenida una primera variable que entra en el proceso, vamos a dar un segundo paso para encontrar otras variables relevante en la explicación del modelo.
pred_i=function(i,k){
vk=c(k0,k)
fml = paste(name_var[8],"~",paste(name_var[vk],
collapse="+"),sep="")
reg=glm(fml,data=datos[-i,],family=binomial)
predict(reg,newdata=datos[i,],
type="response")
}
ROC=function(k){
Y=datos[,8]=="SURVIE"
S=Vectorize(function(i) pred_i(i,k)) (1:length(Y))
R=roc(S,as.factor(Y))
return(list(roc=cbind(R$fpr,R$tpr),
auc=AUC::auc(R)))
}
plot(0:1,0:1,col="white",xlab="",ylab="")
for(k in (1:7)[-k0]) lines(ROC(k)$roc,type="s",col=CL[k])
segments(0,0,1,1,lty=2,col="grey")
legend(.8,.45,
name_var[-k0],
col=CL[-k0],lty=1,cex=.8)
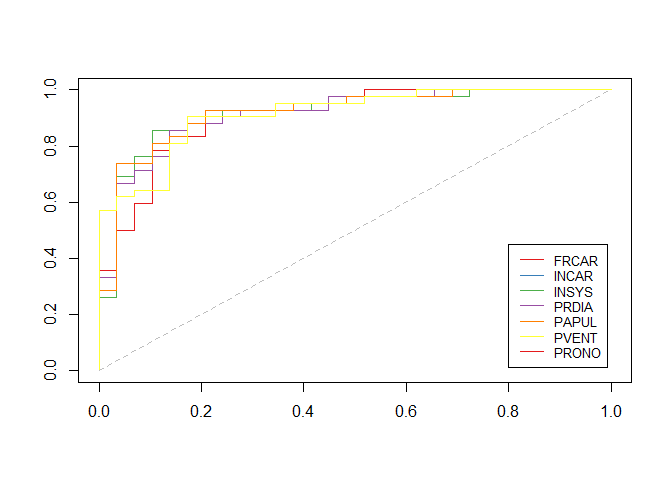
Calculemos los valores del área de la curva de roc de las variables que nos quedan
AUC=rep(NA,7)
for(k in (1:7)[-k0]){
AUC[k]=ROC(k)$auc
cat("Variable ",k,"(",name_var[k],") :",
AUC[k],"\n")
}
## Variable 1 ( FRCAR ) : 0.9064039
## Variable 2 ( INCAR ) : 0.9195402
## Variable 3 ( INSYS ) : 0.9187192
## Variable 4 ( PRDIA ) : 0.9137931
## Variable 5 ( PAPUL ) : 0.9187192
## Variable 6 ( PVENT ) : 0.9137931
Como podemos apreciar los valores son muy similares, y el que mayor valor tiene es INCAR
Si quisiéramos dar otro paso lo haríamos de la siguiente manera
k0=c(k0,which.max(AUC))
pred_i=function(i,k){
vk=c(k0,k)
fml = paste(name_var[8],"~",paste(
name_var[vk],collapse="+"),sep="")
reg=glm(fml,data=datos[-i,],family=binomial)
predict(reg,newdata=datos[i,],
type="response")
}
ROC=function(k){
Y=datos[,8]=="SURVIE"
S=Vectorize(function(i) pred_i(i,k))(1:length(Y))
R=roc(S,as.factor(Y))
return(list(roc=cbind(R$fpr,R$tpr),
auc=AUC::auc(R)))
}
plot(0:1,0:1,col="white",xlab="",ylab="")
for(k in (1:7)[-k0]) lines(ROC(k)$roc,type="s",col=CL[k])
segments(0,0,1,1,lty=2,col="grey")
legend(.8,.45,name_var[-k0],
col=CL[-k0],lty=1,cex=.8)
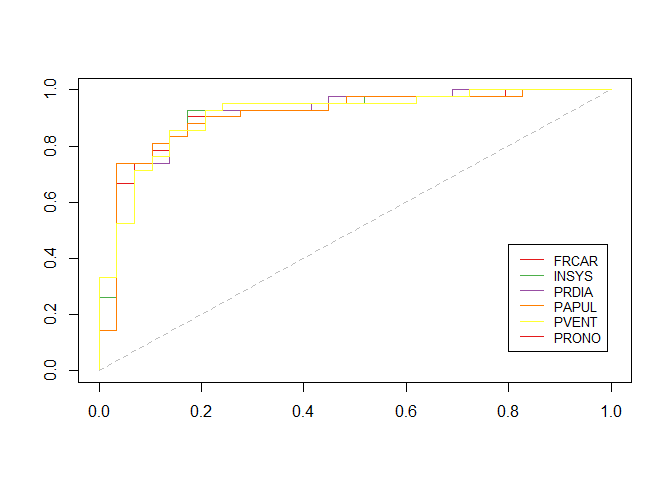
Y los valores de las áreas:
AUC=rep(NA,7)
for(k in (1:7)[-k0]){
AUC[k]=ROC(k)$auc
cat("Variable ",k,"(",name_var[k],") :",
AUC[k],"\n")
}
## Variable 1 ( FRCAR ) : 0.9121511
## Variable 3 ( INSYS ) : 0.9170772
## Variable 4 ( PRDIA ) : 0.910509
## Variable 5 ( PAPUL ) : 0.907225
## Variable 6 ( PVENT ) : 0.909688
NOTA: Este post está basado en esta pagina web.
