Regresión Logit (II)
Contenido
Introducción.
En el post anterior, ya se ha presentado los elementos básicos de un análisis de regresión LOGIT o PROBIT. También se expuso un pequeño ejemplo y las conclusiones que se pueden sacar del mismo. En el presente post voy a seguir utilizando este modelo, pero utilizando ya un ejemplo algo más complicado.
Antes de entrar en materia, voy a explicar dos conceptos estadísticos, que van a servir para medir el nivel de dependencia de unas variables sobre la variable dependiente que se quiere predecir con el modelo. Estos dos conceptos son los denominados WOE (Weight of Evidence) y VI ( information value).
El valor de WOE nos va a facilitar información del poder predictivo de una variable independiente en relación a otra variable dependiente.
El valor de Information value (IV) es una técnica fácil y muy usada para seleccionar variables importantes en el modelo predictivo. A continuación se muestra una tabla que contiene los criterios más utilizados a la hora de aplicar esta técnica.
| Information value (IV) | Capacidad Predicción |
|---|---|
| <=0.02 | No sirve para predicción |
| entre 0.02 y 0.1 | Bajo nivel de predicción |
| entre 0.1 y 0.3 | Nivel predictivo medio |
| entre 0.3 y 0.5 | Alto nivel predicción |
| >= 0.5 | Excelente nivel predicción |
En concreto la fórmula empleada para calcular el valor de WOE es la siguiente:
\[ WOE= \frac{\% No-events \, o \, fracasos}{\% Events \, o\, Éxitos} \]
Es decir y a efectos prácticos, tendremos dos tipos de observaciones, una correspondiente a una variable que toma dos valores (1 y 0) y la otra correspondiente a una variable categórica. Entones a cada valor de la variable categórica le asignamos “Éxito”, si el valor de la variable dicotómica toma el valor 1 o “Fracaso” si el valor de la dicotómica es cero. Con el código que sigue se explica mejor la forma de calcular este indicador estadístico.
El valor de Information Value (IV) se obtiene mediante la aplicación de la siguiente fórmula:
\[ IV=\sum (\% de \, no-events\,o\,fracasos\,-\,\%events \,o\, éxitos)*WOE \]
woe_iv=function(Target,VariableCategorica){
Tabla_WOE=table(VariableCategorica,Target)
DF_WOE=data.frame(FRACASOS=Tabla_WOE[,1],EXITOS=Tabla_WOE[,2])
DF_WOE$EXITOS_PORC=DF_WOE$EXITOS/sum(DF_WOE$EXITOS)
DF_WOE$FRACASOS_PORC=DF_WOE$FRACASOS/sum(DF_WOE$FRACASOS)
DF_WOE$WOE=log(DF_WOE$EXITOS_PORC/DF_WOE$FRACASOS_PORC)
DF_WOE$IV=(DF_WOE$EXITOS_PORC-DF_WOE$FRACASOS_PORC)*DF_WOE$WOE
DF_WOE
}
a<-c(1,1,1,0,0,1,0,1,1,1,0,0,1)
b<-c("a","b","c","a","a","b","b","c","a","b","c","c","c")
woe_iv(a,b)
## FRACASOS EXITOS EXITOS_PORC FRACASOS_PORC WOE IV
## a 2 2 0.250 0.4 -0.47000363 0.070500544
## b 1 3 0.375 0.2 0.62860866 0.110006515
## c 2 3 0.375 0.4 -0.06453852 0.001613463
Otra forma de calcula los valores anteriores es utilizando el paquete InformationValue.
if (!require("InformationValue")) install.packages("InformationValue")
## Loading required package: InformationValue
require("InformationValue")
print("Valores de WOE")
## [1] "Valores de WOE"
WOE(X=as.factor(b),Y=a)
## [1] -0.47000363 0.62860866 -0.06453852 -0.47000363 -0.47000363
## [6] 0.62860866 0.62860866 -0.06453852 -0.47000363 0.62860866
## [11] -0.06453852 -0.06453852 -0.06453852
print("Tabla de valores de WOE y de IV")
## [1] "Tabla de valores de WOE y de IV"
WOETable(X=as.factor(b),a)
## CAT GOODS BADS TOTAL PCT_G PCT_B WOE IV
## 1 a 2 2 4 0.250 0.4 -0.47000363 0.070500544
## 2 b 3 1 4 0.375 0.2 0.62860866 0.110006515
## 3 c 3 2 5 0.375 0.4 -0.06453852 0.001613463
En base a todos los conceptos expuestos anteriormente, vamos a elaborar un ejemplo con 15 variables. Unas son de tipo continuo y otras categóricas (tipo factor en el argot de R), y sobre ellas vamos aplicar los conceptos anteriormente expuestos ( en resumen cálculo de IV), para elegir las variables a priori más influyentes con las que se hará el análisis de regresión logit. Comenzamos por una presentación de los resultados.
#Leemos el fichero
datos2 <- read.csv("./data/adult.csv")
head(datos2)
## AGE WORKCLASS FNLWGT EDUCATION EDUCATIONNUM MARITALSTATUS
## 1 39 State-gov 77516 Bachelors 13 Never-married
## 2 50 Self-emp-not-inc 83311 Bachelors 13 Married-civ-spouse
## 3 38 Private 215646 HS-grad 9 Divorced
## 4 53 Private 234721 11th 7 Married-civ-spouse
## 5 28 Private 338409 Bachelors 13 Married-civ-spouse
## 6 37 Private 284582 Masters 14 Married-civ-spouse
## OCCUPATION RELATIONSHIP RACE SEX CAPITALGAIN CAPITALLOSS
## 1 Adm-clerical Not-in-family White Male 2174 0
## 2 Exec-managerial Husband White Male 0 0
## 3 Handlers-cleaners Not-in-family White Male 0 0
## 4 Handlers-cleaners Husband Black Male 0 0
## 5 Prof-specialty Wife Black Female 0 0
## 6 Exec-managerial Wife White Female 0 0
## HOURSPERWEEK NATIVECOUNTRY ABOVE50K
## 1 40 United-States 0
## 2 13 United-States 0
## 3 40 United-States 0
## 4 40 United-States 0
## 5 40 Cuba 0
## 6 40 United-States 0
La variable denominada ABOVE50k toma solo valores 1 ó 0 y es la que se va a utilizar como variables dependiente para hacer el análisis.
colnames(datos2)
## [1] "AGE" "WORKCLASS" "FNLWGT" "EDUCATION"
## [5] "EDUCATIONNUM" "MARITALSTATUS" "OCCUPATION" "RELATIONSHIP"
## [9] "RACE" "SEX" "CAPITALGAIN" "CAPITALLOSS"
## [13] "HOURSPERWEEK" "NATIVECOUNTRY" "ABOVE50K"
str(datos2)
## 'data.frame': 32561 obs. of 15 variables:
## $ AGE : int 39 50 38 53 28 37 49 52 31 42 ...
## $ WORKCLASS : Factor w/ 9 levels " ?"," Federal-gov",..: 8 7 5 5 5 5 5 7 5 5 ...
## $ FNLWGT : int 77516 83311 215646 234721 338409 284582 160187 209642 45781 159449 ...
## $ EDUCATION : Factor w/ 16 levels " 10th"," 11th",..: 10 10 12 2 10 13 7 12 13 10 ...
## $ EDUCATIONNUM : int 13 13 9 7 13 14 5 9 14 13 ...
## $ MARITALSTATUS: Factor w/ 7 levels " Divorced"," Married-AF-spouse",..: 5 3 1 3 3 3 4 3 5 3 ...
## $ OCCUPATION : Factor w/ 15 levels " ?"," Adm-clerical",..: 2 5 7 7 11 5 9 5 11 5 ...
## $ RELATIONSHIP : Factor w/ 6 levels " Husband"," Not-in-family",..: 2 1 2 1 6 6 2 1 2 1 ...
## $ RACE : Factor w/ 5 levels " Amer-Indian-Eskimo",..: 5 5 5 3 3 5 3 5 5 5 ...
## $ SEX : Factor w/ 2 levels " Female"," Male": 2 2 2 2 1 1 1 2 1 2 ...
## $ CAPITALGAIN : int 2174 0 0 0 0 0 0 0 14084 5178 ...
## $ CAPITALLOSS : int 0 0 0 0 0 0 0 0 0 0 ...
## $ HOURSPERWEEK : int 40 13 40 40 40 40 16 45 50 40 ...
## $ NATIVECOUNTRY: Factor w/ 42 levels " ?"," Cambodia",..: 40 40 40 40 6 40 24 40 40 40 ...
## $ ABOVE50K : int 0 0 0 0 0 0 0 1 1 1 ...
Observamos que básicamente hay dos tipos de variables, unas de tipo int y otras de tipo Factor.
En un problema de clasificación lo ideal es que la variable dependiente ( en este caso ABOVE50 ) esté equilibrada, es decir que aproximadamente tenga el mismo número de casos de uno y otro valor. Veamos en esta ocasión cómo se comporta este factor.
table(datos2$ABOVE50K)
##
## 0 1
## 24720 7841
Como puede verse existe un sesgo claro hacia el valor cero donde se clasifican la mayor parte de los casos. Esta consideración hay que tenerla en cuenta a la hora de proceder a partir la muestra en elementos de los conjuntos train y test. Veamos a continuación cómo lo hacemos en este caso.
# Creamos datos de training y test
input_unos <- datos2[which(datos2$ABOVE50K == 1), ] # Donde están los 1
input_ceros <- datos2[which(datos2$ABOVE50K == 0), ] # Donde están los 0
set.seed(100) # Generamos una semilla
input_unos_training <- sample(1:nrow(input_unos), 0.7*nrow(input_unos))
# sacamos el 70% de los unos para trainig
input_ceros_training <- sample(1:nrow(input_ceros), 0.7*nrow(input_ceros))
# Sacamos una muestra del 70% de ceros
training_unos <- input_unos[input_unos_training, ]
training_ceros <- input_ceros[input_ceros_training, ]
trainingData <- rbind(training_unos, training_ceros)
# junto los unos y los ceros del training
# Creamos los datos del test
test_unos <- input_unos[-input_unos_training, ]
test_ceros <- input_ceros[-input_ceros_training, ]
testData <- rbind(test_unos, test_ceros)
# Junto los unos y los ceros del subconjunto test
Veamos que de esta manera las proporciones se mantienen
print("Proporción en la muestra total")
## [1] "Proporción en la muestra total"
table(datos2$ABOVE50K)/nrow(datos2)
##
## 0 1
## 0.7591904 0.2408096
print("------------------");print("Proporcion en los datos train")
## [1] "------------------"
## [1] "Proporcion en los datos train"
table(trainingData$ABOVE50K)/nrow(trainingData)
##
## 0 1
## 0.7592138 0.2407862
print("------------------");print("Proporción en los datos test")
## [1] "------------------"
## [1] "Proporcion en los datos test"
table(testData$ABOVE50K)/nrow(testData)
##
## 0 1
## 0.759136 0.240864
A continuación vamos a distinguir y separar las variables continuas de las variables de tipo factor.
#Primero los nombre de las variables de tipo factor
Variables_Factor<-c ("WORKCLASS", "EDUCATION", "MARITALSTATUS", "OCCUPATION",
"RELATIONSHIP", "RACE", "SEX", "NATIVECOUNTRY")
#A continuación los nombres de las variables de tipo continuo
Variables_Continua<-c("AGE", "FNLWGT","EDUCATIONNUM", "HOURSPERWEEK", "CAPITALGAIN",
"CAPITALLOSS")
#Creamos a continuación un dataframe vacío que contiene el nombre de las variables
#independientes,y además la columna IV que contendrá el valor de este indicador
iv_df <- data.frame(VARS=c(Variables_Factor, Variables_Continua), IV=numeric(14))
A continuación se muestra el código para tener el valor final de IV para cada una de las variables, información que nos servirá para elegir las variables que entrarán en el análisis.
# El paquete smbbinning
#(https://cran.r-project.org/web/packages/smbinning/smbinning.pdf)
#Sirve entre otras cosas para clacular el IV.
#Además la función smbinning convierte una variable continua en categórica usando el
#método denominado "recursive partitioning"
if (!require("smbinning")) install.packages("smbinning"); require("smbinning")
## Loading required package: smbinning
## Loading required package: sqldf
## Loading required package: gsubfn
## Loading required package: proto
## Loading required package: RSQLite
## Loading required package: partykit
## Loading required package: grid
## Loading required package: libcoin
## Loading required package: mvtnorm
## Loading required package: Formula
# Calculamos IV para las variables categóricas
for(factor_var in Variables_Factor){
smb <- smbinning.factor(trainingData, y="ABOVE50K", x=factor_var) # WOE table
if(class(smb) != "character"){ # heck if some error occured
iv_df[iv_df$VARS == factor_var, "IV"] <- smb$iv
}
}
# Calculamos IV para las variables continuas
for(continuous_var in Variables_Continua){
smb <- smbinning(trainingData, y="ABOVE50K", x=continuous_var) # WOE table
if(class(smb) != "character"){ # any error while calculating scores.
iv_df[iv_df$VARS == continuous_var, "IV"] <- smb$iv
}
}
#Ordenamos las variables por el valor de IV obtenido
(iv_df <- iv_df[order(-iv_df$IV), ] )
## VARS IV
## 5 RELATIONSHIP 1.5435
## 3 MARITALSTATUS 1.3195
## 9 AGE 1.1815
## 11 EDUCATIONNUM 0.7169
## 13 CAPITALGAIN 0.6849
## 12 HOURSPERWEEK 0.4592
## 7 SEX 0.3127
## 1 WORKCLASS 0.1673
## 6 RACE 0.0634
## 2 EDUCATION 0.0000
## 4 OCCUPATION 0.0000
## 8 NATIVECOUNTRY 0.0000
## 10 FNLWGT 0.0000
## 14 CAPITALLOSS 0.0000
Elegimos las variables con mayor valor de IV para hacer la regresión logit
logitMod <- glm(ABOVE50K ~ RELATIONSHIP + MARITALSTATUS+AGE + EDUCATIONNUM,
data=trainingData, family=binomial(link="logit"))
logitMod
##
## Call: glm(formula = ABOVE50K ~ RELATIONSHIP + MARITALSTATUS + AGE +
## EDUCATIONNUM, family = binomial(link = "logit"), data = trainingData)
##
## Coefficients:
## (Intercept) RELATIONSHIP Not-in-family
## -6.94905 -0.14158
## RELATIONSHIP Other-relative RELATIONSHIP Own-child
## -1.42163 -1.68403
## RELATIONSHIP Unmarried RELATIONSHIP Wife
## -0.55419 0.11067
## MARITALSTATUS Married-AF-spouse MARITALSTATUS Married-civ-spouse
## 2.12634 1.76785
## MARITALSTATUS Married-spouse-absent MARITALSTATUS Never-married
## -0.11044 -0.36931
## MARITALSTATUS Separated MARITALSTATUS Widowed
## -0.12247 -0.30445
## AGE EDUCATIONNUM
## 0.02301 0.37877
##
## Degrees of Freedom: 22791 Total (i.e. Null); 22778 Residual
## Null Deviance: 25160
## Residual Deviance: 17230 AIC: 17260
summary(logitMod)
##
## Call:
## glm(formula = ABOVE50K ~ RELATIONSHIP + MARITALSTATUS + AGE +
## EDUCATIONNUM, family = binomial(link = "logit"), data = trainingData)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.3136 -0.6263 -0.2703 -0.0594 3.7678
##
## Coefficients:
## Estimate Std. Error z value
## (Intercept) -6.949048 0.341848 -20.328
## RELATIONSHIP Not-in-family -0.141583 0.312673 -0.453
## RELATIONSHIP Other-relative -1.421634 0.296227 -4.799
## RELATIONSHIP Own-child -1.684027 0.313906 -5.365
## RELATIONSHIP Unmarried -0.554188 0.324738 -1.707
## RELATIONSHIP Wife 0.110668 0.070765 1.564
## MARITALSTATUS Married-AF-spouse 2.126340 0.634987 3.349
## MARITALSTATUS Married-civ-spouse 1.767849 0.316306 5.589
## MARITALSTATUS Married-spouse-absent -0.110436 0.235376 -0.469
## MARITALSTATUS Never-married -0.369309 0.091450 -4.038
## MARITALSTATUS Separated -0.122470 0.169112 -0.724
## MARITALSTATUS Widowed -0.304449 0.159086 -1.914
## AGE 0.023013 0.001655 13.907
## EDUCATIONNUM 0.378765 0.008636 43.858
## Pr(>|z|)
## (Intercept) < 0.0000000000000002 ***
## RELATIONSHIP Not-in-family 0.650682
## RELATIONSHIP Other-relative 0.0000015936 ***
## RELATIONSHIP Own-child 0.0000000811 ***
## RELATIONSHIP Unmarried 0.087902 .
## RELATIONSHIP Wife 0.117849
## MARITALSTATUS Married-AF-spouse 0.000812 ***
## MARITALSTATUS Married-civ-spouse 0.0000000228 ***
## MARITALSTATUS Married-spouse-absent 0.638934
## MARITALSTATUS Never-married 0.0000538229 ***
## MARITALSTATUS Separated 0.468946
## MARITALSTATUS Widowed 0.055654 .
## AGE < 0.0000000000000002 ***
## EDUCATIONNUM < 0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 25162 on 22791 degrees of freedom
## Residual deviance: 17234 on 22778 degrees of freedom
## AIC: 17262
##
## Number of Fisher Scoring iterations: 7
A continuación calculamos las predicciones mediante dos fórmulas.
predicted1 <- plogis(predict(logitMod, testData)) # Prediccion de los datos test
head(predicted1)
## 9 12 26 39 56 64
## 0.1909527 0.6066212 0.7371995 0.3362275 0.4003521 0.8636073
# o
predicted2 <- predict(logitMod, testData, type="response") # Prediccion de los datos test
head(predicted1)
## 9 12 26 39 56 64
## 0.1909527 0.6066212 0.7371995 0.3362275 0.4003521 0.8636073
Como podemos observar el valor devuelto tanto por uno como por otro método es una probabilidad. Para clasificar las respuestas como 0 ó 1 (posibles valores de la variable dependiente), inicialmente se podría pensar que si p<0.5 se asigna cero y en caso contrario un uno. Pero esta es una decisión opinática y fácil de usar pero sin ningún criterio claro. Para optimizar la elección de este valor de corte, se puede usar la función optimalCuttof del paquete InformationValue que previamente ya se ha cargado en este ejemplo.
if (!require("InformationValue")) install.packages("InformationValue")
require("InformationValue")
(PuntoCorte<-optimalCutoff(testData$ABOVE50K,predicted2)[1])
## [1] 0.5382003
Si ahora se quiere obtener la predicción real ( es decir valores cero ó uno ), se haría de la siguiente manera.
predic<-ifelse(predicted2>PuntoCorte,1,0)
head(predic)
## 9 12 26 39 56 64
## 0 1 1 0 0 1
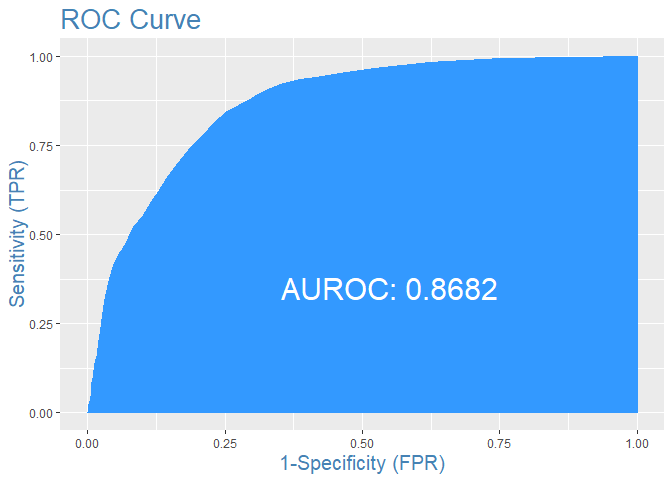
Si quisiéramos sacar la curva de ROC para el modelo obtenido se haría de la siguiente manera. El gráfico también muestra el área bajo la curva, de tal manera que cuanto más área, mejor clasificación se obtiene. En este caso concreto, quizá se podría mirar si introduciendo alguna variable se puede conseguir mejorar la clasificación obtenida.
plotROC(testData$ABOVE50K,predicted1)