Primeros pasos con R
Contenido
- Introducción
- Vectores y asignaciones.
- Operaciones con vectores.
- Generación de secuencias regulares.
- Operaciones lógicas.
- Matrices en R
- Funciones cbind() y rbind().
- Dataframes.
- Funciones de probabilidad.
- Instalación de paquetes.
Introducción
Indudablemente exponer todas las posibilidades que nos ofrece R en un post sería una tarea totalmente imposible, dado que R cuenta con una gran cantidad de librerías o packages ( se pueden ver en este enlace ), además existen otras muchas que se pueden descargar desde otros muchos lugares de Internet, incluyendo a Github. Entre las librerías más utilizadas en R, se pueden destacar las que se muestran en el siguiente enlace.
Por ese motivo, en lo que sigue me limitaré a hacer una pequeña introducción a los elementos más utilizados en R, con la finalidad de que el lector se vaya familiarizando con este lenguaje. Para profundizar más sobre ello, existen muchos tutoriales en Internet que facilitan este aprendizaje, uno de ellos y además en español se puede ver en este enlace.
Vectores y asignaciones.
Uno de los elementos más utilizados por parte de R son los vectores, que no son más que conjuntos de datos, todos ellos del mismo tipo. Para incluir un vector a una variable determinada se utiliza el símbolo “<-“ o también está permitido utilizar “=”. Una de las formas más utilizadas para crear un vector es utilizando la expresión c(….), pero para aclarar esto mejor se ve con el siguiente ejemplo:
x<-c(2.3,4.6,6.2,3.1,2.3) # Asignación vector a una variable
print(x)
## [1] 2.3 4.6 6.2 3.1 2.3
Se pueden extraer elementos concretos del vector ( a diferencia de Python donde el índice de los elementos comienza en 1, en R ese índice comienza en 1). A continuación se muestra ejemplo sobre cómo entresacar algunos elementos del vector anteriormente definido:
print(paste("El primer elemento del vector es",x[1]))
## [1] "El primer elemento del vector es 2.3"
print(paste("El tercer elemento del vector es",x[3]))
## [1] "El tercer elemento del vector es 6.2"
También existe la posibilidad de suprimir algún elemento del vector, para ello hay que hacer referencia a ese elemento pero con signo negativo. Veamoslo en el siguiente ejemplo:
print(x)
## [1] 2.3 4.6 6.2 3.1 2.3
x1<-x[-2]
print("Sin el segundo elemento del vector quedaría:")
## [1] "Sin el segundo elemento del vector quedaría:"
print(x1)
## [1] 2.3 6.2 3.1 2.3
Otras formas de hacer asignaciones de valores, se pueden ver en los siguientes ejemplos:
x=c(2.3,4.6,6.2,3.1,2.3) #Se utiliza el operador de asignación 0
assign("x",c(2.3,4.6,6.2,3.1,2.3)) #Utilizando función assign
c(2.3,4.6,6.2,3.1,2.3)->x #Sentido flecha invertido
#También se pueden unir vectores
y<-c(x,c(0,0,0),x)
y
## [1] 2.3 4.6 6.2 3.1 2.3 0.0 0.0 0.0 2.3 4.6 6.2 3.1 2.3
Operaciones con vectores.
Las operaciones más usuales que se pueden hacer con vectores son las siguientes:
- suma(+),resta(-),multiplicación(*),división(\) y exponenciación(^)
- Funciones aritméticas: log, exp, sin, cos, tan, sqrt, etc.
- Máximo (max), Mínimo (min),rango(range)
- Longitud del vector (número de elementos):length(…)
- Producto y suma elemento a elemento. prod(),sum()
- Media y varianza. mean(), var()
Otra de las operaciones que se utiliza con cierta frecuencia es la ordenación de un vector. Para ello se puede utilizar la función sort.
x<-c(4,2,7,3,8,5)
print(sort(x))
## [1] 2 3 4 5 7 8
Otra forma de hacer una ordenación de un vector es utilizando la función order que nos devuelve el indice de los elementos pero ordenados.
print(order(x))
## [1] 2 4 1 6 3 5
#Observamos que el segundo valor es el mínimo, despues viene el cuarto valor, etc.
#Ahora utilizo las posiciones dadas anteriormente para odenar el vector
print("La ordenación usando la función order sería:")
## [1] "La ordenación usando la función order sería:"
a<-order(x)
print(x[a])
## [1] 2 3 4 5 7 8
Para entender con claridad, el proceso que sigue R para hacer la ordenación, primero hay que conocer, cómo R puede cambiar el orden de colocación de los elementos de un vector. Para ello, supongamos que tenemos un vector con cuatro elementos y queremos intercalar el primero con el segundo y el tercero con el cuarto. Esto se ve con detalle en el siguiente ejemplo:
x<-c(5,3,2,7)
x1<-x[c(2,1,4,3)]
#El vector c(2,1,4,3) indica las posiciones que queremos aparezcan
print(x)
## [1] 5 3 2 7
print("se intercambia primero con segundo y tercero con cuarto")
## [1] "se intercambia primero con segundo y tercero con cuarto"
print(x1)
## [1] 3 5 7 2
Generación de secuencias regulares.
En el apartado anterior se ha mostrado cómo poder crear vectores en R. Ahora bien si por diferentes motivos, se desea crear vectores con muchos elementos y que además siguen una pauta de generación regular, el procedimiento indicado anteriormente es difícil de utilizar para conseguir este objetivo. Para esto R ofrece una serie de funciones que permiten generar vectores con una serie de valores que siguen una pauta regular en su generación. A continuación se muestran estas funciones, muy utilizadas dentro de R.
Supongamos que queremos construir una secuencia de números consecutivos del 5 al 15, por ejemplo. En el siguiente ejemplo se muestra el operador “:” que permite obtener dicha secuencia:
a<-5:15
print(a)
## [1] 5 6 7 8 9 10 11 12 13 14 15
Hay que tener en cuenta que el operador “:” tiene prioridad sobre el resto de operaciones. Veamos esto en el siguiente ejemplo.
(2*3:10) #Observar que poner un paréntesis es equivalente (no igual) a usar la función print
## [1] 6 8 10 12 14 16 18 20
#Lo anterior primero calcula 3:10 y el resultado lo multiplica por 2
print("cambiamos la prioridad con un paréntesis")
## [1] "cambiamos la prioridad con un paréntesis"
(2*3):10
## [1] 6 7 8 9 10
#Lo anterior, primero calcula 2*3 y luego calcula 6:10
Si queremos una secuencia decreciente, lo haríamos de la siguiente manera:
(10:1)
## [1] 10 9 8 7 6 5 4 3 2 1
Otra función muy utilizada para generar secuencias es la función seq(), cuya sintaxis es la siguiente:
seq(from=value,to=value,by=value,length.out=value,along=vector)
print(seq(1,5))
## [1] 1 2 3 4 5
print(seq(1,14,by=2)) #Va de dos en dos
## [1] 1 3 5 7 9 11 13
print(seq(1,6,length.out = 4)) #Cuatro números equiespaciados
## [1] 1.000000 2.666667 4.333333 6.000000
print(seq(1,12,along.with = c(4,2,5)))
## [1] 1.0 6.5 12.0
#saca tres números equiespaciados pues length(c(4,2,5)) es tres
print(seq(1,10,by=3))
## [1] 1 4 7 10
Se puede generar un vector con la función rep(). Veamos un ejemplo:
x<-c(3,6,4,7,2)
print(rep(x,times=3))
## [1] 3 6 4 7 2 3 6 4 7 2 3 6 4 7 2
print(rep(x,each=3)) #Repite cada número tres veces
## [1] 3 3 3 6 6 6 4 4 4 7 7 7 2 2 2
Operaciones lógicas.
Se utilizan para poder hacer comparaciones. Una variable de tipo Lógica puede tomar los valores TRUE o FALSE, como se puede ver en el siguiente ejemplo:
x<-3
print(x>2)
## [1] TRUE
print(x<2)
## [1] FALSE
Para hacer comparaciones entre elementos se utilizan los operadores lógicos, los cuales son los siguientes:
- < Operador menor que
- <= Operador menor o igual que
- > Operador mayor que
- >= Operador mayor o igual que
- == Operador igualdad
- != Operador distinto que
Para enlazar varios elementos de comparación se utilizan los siguientes operadores lógicos:
- AND (&)
-
OR ( ) - NOT (!)
Matrices en R
Un matriz es otro elemento de trabajo de R, que realmente es similar a un vector, con la particularidad de que tiene un atributo añadido denominado dim(), que en el caso de dos dimensiones indica el número de filas y de columnas.
Veamos a continuación algunos ejemplos sobre cómo poder construir las matrices en R.
print(matrix(4,ncol = 5,nrow = 4))
## [,1] [,2] [,3] [,4] [,5]
## [1,] 4 4 4 4 4
## [2,] 4 4 4 4 4
## [3,] 4 4 4 4 4
## [4,] 4 4 4 4 4
print(matrix(1:10,ncol = 3)) #Por defecto la construye por columnas
## Warning in matrix(1:10, ncol = 3): la longitud de los datos [10] no es un
## submúltiplo o múltiplo del número de filas [4] en la matriz
## [,1] [,2] [,3]
## [1,] 1 5 9
## [2,] 2 6 10
## [3,] 3 7 1
## [4,] 4 8 2
print(matrix(1:9,ncol = 3, byrow = TRUE)) #Construcción por filas
## [,1] [,2] [,3]
## [1,] 1 2 3
## [2,] 4 5 6
## [3,] 7 8 9
Podemos construir una matriz desde un vector de la siguiente manera:
a<-1:2000 #Construimos un vector de 2000 elementos
print("a inicialmente es un vector con tipos de datos enteros")
## [1] "a inicialmente es un vector con tipos de datos enteros"
print(class(a))
## [1] "integer"
# Lo cambiamos ahora a una matriz de una dimensión determinada.
dim(a)<-c(2,4,250)
print("Ahora a es un array")
## [1] "Ahora a es un array"
print(class(a))
## [1] "array"
#Si queremos sacar un solo elemento:
print(a[2,3,6])
## [1] 46
#Si queremos sacar un subconjunto, se utiliza el operador :
print(a[2,2,6:8])
## [1] 44 52 60
Funciones cbind() y rbind().
Cuando se tienen varias matrices (aunque esto también sirve para los dataframes), las misma se pueden unir bien por filas o por columnas, para obtener otra nueva matriz. La unión por filas se hace con la función rbind() y para la unión por columnas se emplea cbind(). Veamos un ejemplo de cada uno de estos casos.
print("Primero unión por columnas")
## [1] "Primero unión por columnas"
a<-matrix(c(1,2,3,4,5,5),ncol = 3,nrow = 2)
print(a)
## [,1] [,2] [,3]
## [1,] 1 3 5
## [2,] 2 4 5
b<-matrix(c(8,9,10,11),ncol = 2, nrow = 2)
print(b)
## [,1] [,2]
## [1,] 8 10
## [2,] 9 11
c<-cbind(a,b) #la columnas de b se añaden a las de a
print(c)
## [,1] [,2] [,3] [,4] [,5]
## [1,] 1 3 5 8 10
## [2,] 2 4 5 9 11
print("Despues unión por filas")
## [1] "Despues unión por filas"
a<-matrix(c(1,2,3,4,5,5),ncol = 2,nrow = 3)
print(a)
## [,1] [,2]
## [1,] 1 4
## [2,] 2 5
## [3,] 3 5
b<-matrix(c(8,9,10,11),ncol = 2, nrow = 2)
print(b)
## [,1] [,2]
## [1,] 8 10
## [2,] 9 11
c<-rbind(a,b) #Las filas de b se añaden a las de a
print(c)
## [,1] [,2]
## [1,] 1 4
## [2,] 2 5
## [3,] 3 5
## [4,] 8 10
## [5,] 9 11
Dataframes.
Los Dataframes en R son uno de los elementos más utilizados y están constituidos por un conjunto de filas y columnas, similar a las matrices, pero en esta caso los elementos de cada columna deben ser iguales para una columna determinada pero no todas las columnas deben tener el mismo tipo de elemento. Es decir una columna puede contener enteros, otra cadena de caracteres, ect.
Una forma de construir un Dataframe puede ser la siguiente:
datos<-data.frame(primera=c(1,2,3,4),segunda=c('a','b','c','d'),tercera=c(1.2,3.5,2.7,5.8))
print(datos)
## primera segunda tercera
## 1 1 a 1.2
## 2 2 b 3.5
## 3 3 c 2.7
## 4 4 d 5.8
Podemos sacar información de un Dataframe de la siguiente manera:
print(datos[,1:2])
## primera segunda
## 1 1 a
## 2 2 b
## 3 3 c
## 4 4 d
# Toda una columna como un vector
print("Sólo una columna")
## [1] "Sólo una columna"
print(datos$primera)
## [1] 1 2 3 4
Funciones de probabilidad.
El paquete R tiene una finalidad claramente estadística y por lo tanto cuenta con una amplia gama de funciones que permiten operar con las funciones de densidad de cualquier tipo de distribución.
En la tabla que sigue, se muestra en la columna de la izquierda la distribuciones más utilizadas de las variables aleatorias, mientras que en la columna de la derecha figura el nombre con la que R se refiere a esas distribuciones.
| Distribución | Denominación R |
|---|---|
| Gauss ó Normal | norm |
| Exponencial | exp |
| Gamma | gamma |
| Poisson | pois |
| Weibull | weibull |
| Cauchy | cauchy |
| Beta | beta |
| t-student | t |
| Fisher–Snedecor (F) | f |
| Chi-cuadrado | chisq |
| Binomial | binom |
| Geométrica | geom |
| Hipergeométrica | hyper |
| Logística | logis |
| Lognormal | lnorm |
| Binomial Negativa | nbinom |
| Uniforme | unif |
| Estadís. Wilcoxon | wilcox |
Las funciones de R que operan con estas distribuciones tienen en común una letra (r,d,q ó p) que antecede al nombre de la distribución, y cuyo significado es el siguiente:
-
r ( proviene de random), permite generar números aleatorios de una distribución concreta. Por ejemplo rnorm(200,mean=4,sd=1) genera 200 números aleatorios de una distribución normal de media 4 y desviación típica 1.
-
d ( de función de densidad). Nos da el valor que tiene la función de densidad. Por ejemplo dnorm(3,mean=2,sd=1), nos da el valor de la función de densidad en 3 para una distribución normal de media 2 y desviación típica de 1.
-
q ( de quartil). Nos da el valor del quartil ( valor del eje x que deja a la izquierda una masa igual al argumento de la función). Por ejemplo qnorm(0.4,mean=2,sd=1), nos daría el valor de la abscisa que deja una masa de 0.4 en una distribución normal de media 2 y desviación típica de 1.
-
p ( de probabilidad).Nos daría el valor de la función de distribución acumulada en un determinado punto. Es decir, para una variable X nos daría P[X<=t]. Por ejemplo pnorm(2,mean=1,sd=1) nos daría P[X<=2] En una distribución normal de media 1 y desviación típica de 1.
Veamos algunos ejemplos de esto, para una distribución normal.
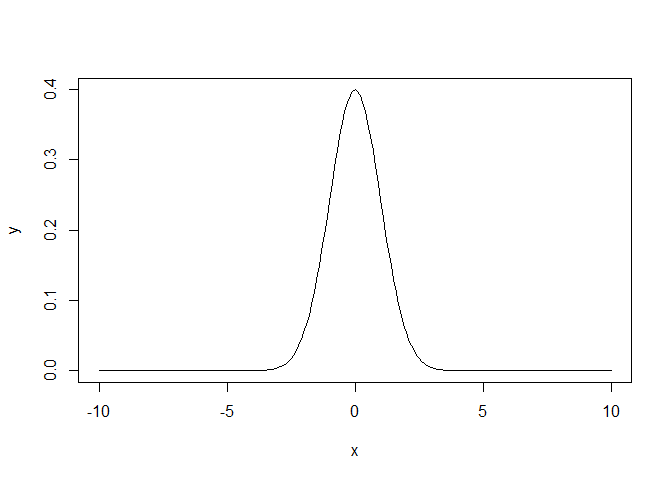
# Primero para d
x <-seq(-10,10,by=.1)
y<-dnorm(x) #Valor de la densidad para una normal(0,1)
plot(x,y,type='l')
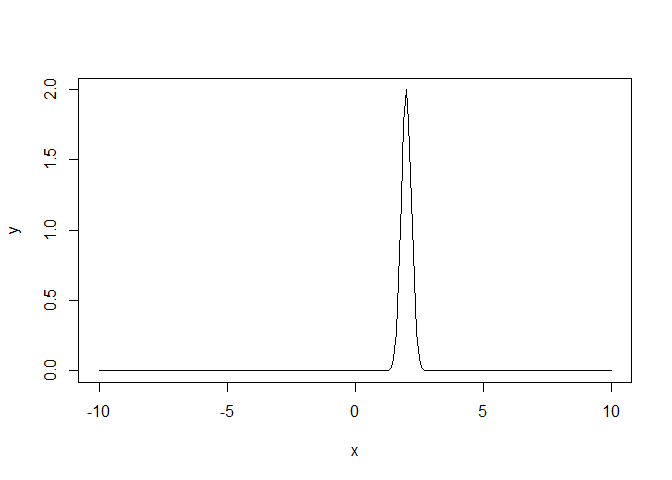
# Lo mismos pero una ditribución normal(2,0.2)
x <-seq(-10,10,by=.1)
y<-dnorm(x,mean = 2,sd=0.2)
plot(x,y,type='l')
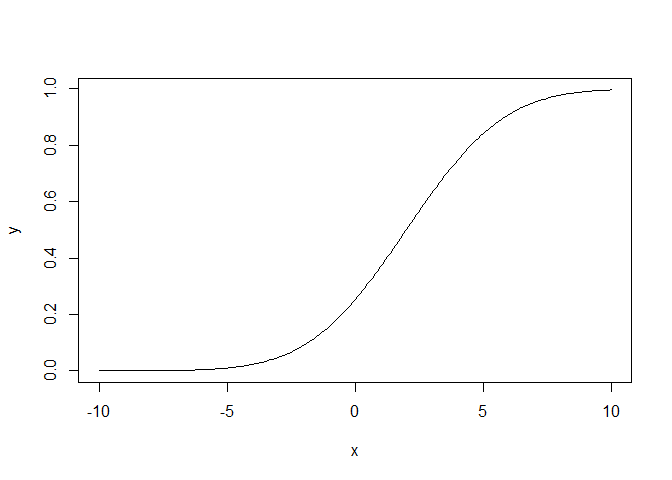
Para la función de distribución acumulada.
x <-seq(-10,10,by=.1)
y<-pnorm(x,mean = 2,sd=3)
plot(x,y,type='l')
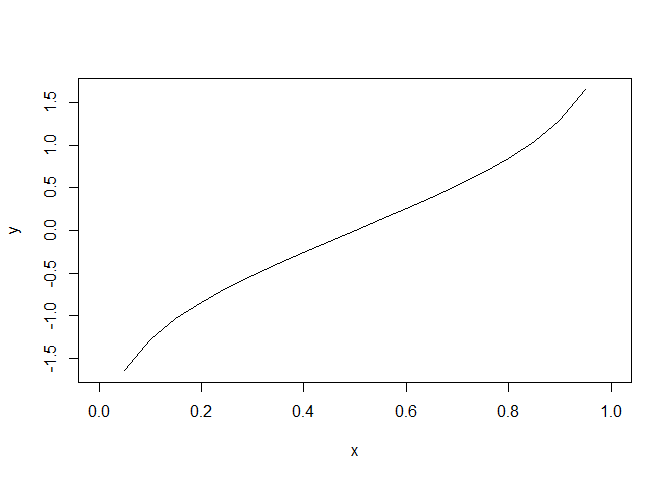
Ahora para los cuantiles.
x <-seq(0,1,by=.05)
y<-qnorm(x)
plot(x,y,type='l')
Ahora la generación de números aleatorios de una distribución normal
y<-rnorm(200)
hist(y) #Representamos el histograma
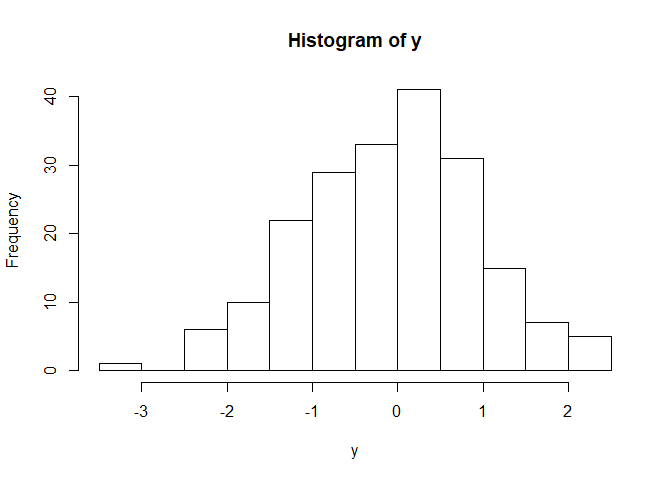
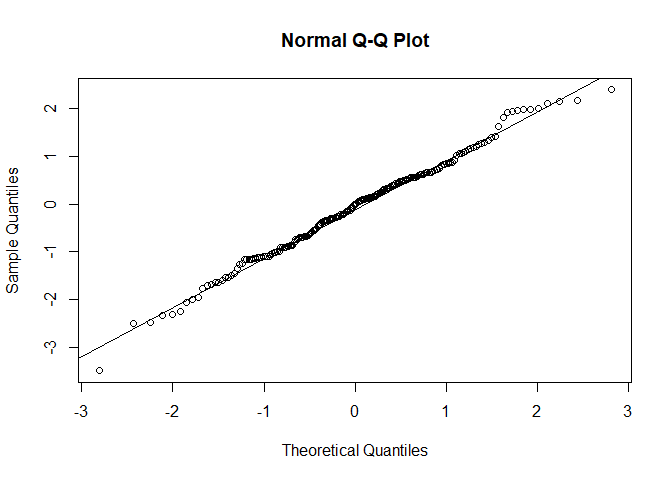
Las dos funciones que siguen se suelen usar a menudo para el contraste de normalidad, y lo que hace es comparar los cuantiles empíricos con los cuantiles teóricos. En este caso dado que los puntos se distribuyen bien a los largo de la línea diagonal, se podría concluir que los datos se ajustan razonablemente bien a una distribución normal.
qqnorm(y)
qqline(y)
Instalación de paquetes.
Cuando se instala R, por defecto se cargan un serie de paquetes que no cubren necesariamente todas las necesidades de los usuarios finales. Por ello se hace necesario proceder a cargar en cada momento los paquetes que se necesiten y que por defecto no se hayan cargado en R.
Para ver los paquetes instalados por defecto, bien se puede mirar en la parte inferior de Rstudio en la pestaña “Packages”, o bien se puede ejecutar la siguiente instrucción:
getOption("defaultPackages")
## [1] "datasets" "utils" "grDevices" "graphics" "stats" "methods"
Posteriormente los paquetes se instalarán con la instrucción:
install.package( )
Con la instrucción anterior lo que se hace es descargar el paquete en nuestro equipo, para que el mismo quede listo para cuando lo necesitemos. Para cargar el paquete en la memoria del ordenador y lo podamos usar se utiliza uno de las dos instrucciones siguientes:
- library()
- require()
Si estamos escribiendo un script de código R que necesite cargar un paquete con la instrucción install.package() cada vez que ejecutemos el código, se va a emplear un tiempo determinado para descargar el paquete desde la red. Para evitar, lo que se hace es comprobar si el paquete ya esta o no descargado, si no está lo descarga y después lo carga en memoria. Si ya está descargado de la red se hace la carga directamente. Para conseguir esto se utiliza la siguiente instrucción ( en este ejemplo concreto para cargar la librería MASS).
if(!require(MASS)){install.packages("MASS")};require(MASS)
