Parámetro C en Clasificación
Contenido
Introducción
En post anteriores, se ha explicado los métodos existentes para trabajar con modelos de regresión logística, tanto con python como con R. En el caso de tabajar con Python y en concreto con scikit-learn, ya se ha comentado que existe un parámetro C que va a servir para ajustar mejor el modelo y evitar bien un subajuste o bien un sobreajuste (overfiting). En el presente post, se va a hacer una pequeña exposición que seguro servirá para aclarar la utilidad de este parámetro C.
Comenzamos como siempre por importar unas determinadas librerías.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
Para la exposición que quiero hacer en este post, va a ser muy útil el fichero “Iris” que ya viene cargado dentro de scikip- learn. Y además por cuestiones meramente didácticas vamos a separar las dos features correspondientes a sepal, de las otras dos features correspondientes a los sépalos.
from sklearn import datasets
iris = datasets.load_iris()
X1_sepal = iris.data[:,[0,1]]
X2_petal = iris.data[:,[2,3]]
y = iris.target
print(X1_sepal[1:5,:])
print(X2_petal[1:5,:])
print(y)
[[4.9 3. ]
[4.7 3.2]
[4.6 3.1]
[5. 3.6]]
[[1.4 0.2]
[1.3 0.2]
[1.5 0.2]
[1.4 0.2]]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
Veamos a continuación cómo quedan distribuidos los datos
plt.figure(figsize=(15, 5))
plt.subplot(1,2,1)
plt.scatter(X1_sepal[:, 0], X1_sepal[:, 1], c=y)
plt.xlabel('Longitud Sépalo')
plt.ylabel('Anchura Sépalo')
plt.title("Sépalos")
plt.subplot(1,2,2)
plt.scatter(X2_petal[:, 0], X2_petal[:, 1], c=y)
plt.xlabel('Longitud Pétalo')
plt.ylabel('Anchura Pétalo')
plt.title("Pétalos")
Text(0.5,1,'Pétalos')
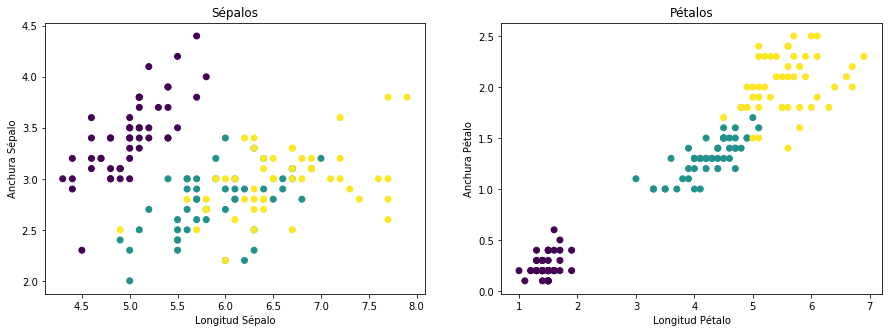
Observamos que en el caso de los sépalos hay puntos de dso categorías mezclados, por lo que hacer una clasificación con un modelo logit, puede ser bastante complicado, ya que este modelo es de tipo lineal, y un modelo de estas características dificilmente va a segregar ese tipo de puntos. No ocurre así en el caso del gráfico de los Pétalos, donde los puntos están más diferenciasdos por categorías.
Vamos a crear una función que va a ser muy útil para calcular las regiones de decisión.
from matplotlib.colors import ListedColormap
def plot_decision_regions(X,y,classifier,test_idx=None,resolution=0.02):
# inicializamos las marcas utilizadas
markers = ('s','x','o','^','v')
colors = ('red','blue','lightgreen','gray','cyan')
color_Map = ListedColormap(colors[:len(np.unique(y))]) #Se cogen tantos colores como la cantidad categorías
#tiene la variable independiente y
# Delimitamos el área donde se dibujará
x1_min = X[:,0].min() - 1
x1_max = X[:,0].max() + 1
x2_min = X[:,1].min() - 1
x2_max = X[:,1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),
np.arange(x2_min,x2_max,resolution))
Z = classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contour(xx1,xx2,Z,alpha=0.4,cmap = color_Map)
plt.xlim(xx1.min(),xx1.max())
plt.ylim(xx2.min(),xx2.max())
# Seleccionamos los elementos de tipo test
X_test, Y_test = X[test_idx,:], y[test_idx]
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x = X[y == cl, 0], y = X[y == cl, 1],
alpha = 0.8, c = color_Map(idx),
marker = markers[idx], label = cl
)
División y escalado de los datos
from sklearn.cross_validation import train_test_split
from sklearn.preprocessing import StandardScaler
############################################################# DIVIDIENDO
X_train_sepal, X_test_sepal, y_train_sepal, y_test_sepal = train_test_split(X1_sepal,y,test_size=0.3,random_state=0)
print("# elementos training sepal: ", len(X_train_sepal))
print("# elementos test sepal: ", len(X_test_sepal))
X_train_petal, X_test_petal, y_train_petal, y_test_petal = train_test_split(X2_petal,y,test_size=0.3,random_state=0)
print("# elemenos training petal: ", len(X_train_petal))
print("# elementos testing petal: ", len(X_test_petal))
########################################################### SCALANDO
sc = StandardScaler()
X_train_sepal_std = sc.fit_transform(X_train_sepal)
X_test_sepal_std = sc.transform(X_test_sepal)
sc = StandardScaler()
X_train_petal_std = sc.fit_transform(X_train_petal)
X_test_petal_std = sc.transform(X_test_petal)
#########################################COMBINANDO PARA PLOT'S FUTUROS
X_combined_sepal_standard = np.vstack((X_train_sepal_std,X_test_sepal_std))
Y_combined_sepal = np.hstack((y_train_sepal, y_test_sepal))
X_combined_petal_standard = np.vstack((X_train_petal_std,X_test_petal_std))
Y_combined_petal = np.hstack((y_train_petal, y_test_petal))
# elementos training sepal: 105
# elementos test sepal: 45
# elemenos training petal: 105
# elementos testing petal: 45
El parámetro C incide de una forma importante en la configuración del modelo, de tal manera que si C es muy pequeño, entonces de incrementa la “regularization strength” y por lo tanto se obtiene un modelo simple que infraajusta los datos. Situación contraria se tiene en el supuesto de que C sea muy grande, ya que en este caso se baja el poder de regularization y se incrementa la complegidad del modelo obteniéndose de esta manera un sobreajuste de dos datos (overfiting).
Veamos primero lo que ocurre en el caso de los sépalos.
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.learning_curve import validation_curve
C_param_range = [0.001,0.01,0.1,1,10,100]
sepal_acc_table = pd.DataFrame(columns = ['C_parameter','Accuracy'])
sepal_acc_table['C_parameter'] = C_param_range
plt.figure(figsize=(10, 10))
j = 0
for i in C_param_range:
# Generamos un modelo de regresión logit
lr = LogisticRegression(penalty = 'l2', C = i,random_state = 0)
lr.fit(X_train_sepal_std,y_train_sepal)
# Predecimos el modelo
y_pred_sepal = lr.predict(X_test_sepal_std)
# Sacamos la acuracidad
sepal_acc_table.iloc[j,1] = accuracy_score(y_test_sepal,y_pred_sepal)
j += 1
# Imprimimos los datos
plt.subplot(3,2,j)
plt.subplots_adjust(hspace = 0.4)
plot_decision_regions(X = X_combined_sepal_standard
, y = Y_combined_sepal
, classifier = lr
, test_idx = range(105,150))
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('C = %s'%i)
D:\programas\Anaconda\lib\site-packages\sklearn\learning_curve.py:22: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the functions are moved. This module will be removed in 0.20
DeprecationWarning)
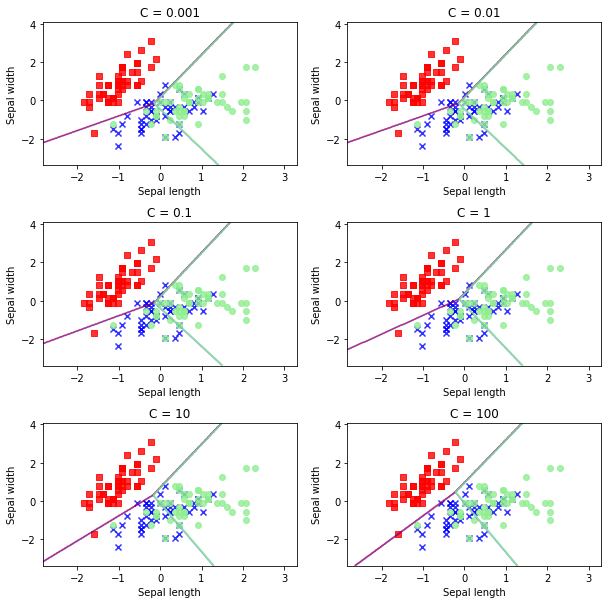
Como puede observarse, existe poca diferencia entre los modelos obtenidos, lo cual es debido a que un modelo de regresión logit es de tipo lineal, como ya se ha dicho anteriormente, y por lo tanto dificilmente va a ajustarse en los datos que están mezclados.
Hagamos a continuación algo similar para los pétalos.
petal_acc_table = pd.DataFrame(columns = ['C_parameter','Accuracy'])
petal_acc_table['C_parameter'] = C_param_range
plt.figure(figsize=(10, 10))
j = 0
for i in C_param_range:
# Aplicamos el modelo de regresión
lr = LogisticRegression(penalty = 'l2', C = i,random_state = 0)
lr.fit(X_train_petal_std,y_train_petal)
# Hacemos la predicción
y_pred_petal = lr.predict(X_test_petal_std)
# Sacamos los scores
petal_acc_table.iloc[j,1] = accuracy_score(y_test_petal,y_pred_petal)
j += 1
# Dibujamos las regiones de decisión
plt.subplot(3,2,j)
plt.subplots_adjust(hspace = 0.4)
plot_decision_regions(X = X_combined_petal_standard
, y = Y_combined_petal
, classifier = lr
, test_idx = range(105,150))
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.title('C = %s'%i)
![png]./img/jupyter/2018-09-11-Parameter_C/(output_14_0.png)
En este caso, la situación cambia ostensiblemente en relación con lo visto en el caso anterior. En este caso un valor de C muy pequeño origina una clasificación bastante pobre (infraajuste), mientras que a medida que C se incrementa el ajuste es menor, pero ojo porque se puede caer en un sobreajuste, nada aconsejable para este tipo de trabajos.
Una cuestión muy importante a la hora de decidir el valor más adecuado de C es qué método utilizar para au elección. La idea es intentar que la acuracidad tanto para los datos de entrenamiento como para los de test sea similares, y para ello la herramienta qu proporciona scikit learn son las curvas de validación.
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.learning_curve import validation_curve
### 1. Use of validation curves for both datasets.
C_param_range = [0.001,0.01,0.1,1,10,100,1000]
plt.figure(figsize=(15, 10))
# Se aplica un modelo de regresión logística
lr = LogisticRegression(penalty='l2',C = i,random_state = 0)
# Plot de SEPALOS, curva de validación
train_sepal_scores, test_sepal_scores = validation_curve(estimator=lr
,X=X_combined_sepal_standard
,y=Y_combined_sepal
,param_name='C'
,param_range=C_param_range
)
train_sepal_mean = np.mean(train_sepal_scores,axis=1)
train_sepal_std = np.std(train_sepal_scores,axis=1)
test_sepal_mean = np.mean(test_sepal_scores,axis=1)
test_sepal_std = np.std(test_sepal_scores,axis=1)
plt.subplot(2,2,1)
plt.plot(C_param_range
,train_sepal_mean
,color='blue'
,marker='o'
,markersize=5
,label='training acuracidad')
plt.plot(C_param_range
,test_sepal_mean
,color='green'
,marker='x'
,markersize=5
,label='test acuracidad')
plt.title('Curva validación para SEPALOS')
plt.xlabel('C_parametro')
plt.ylabel('Acuracidad')
plt.legend(loc='lower right')
plt.ylim([0.5,1])
# Curva de validación para PETALOS
train_petal_scores, test_petal_scores = validation_curve(estimator=lr
,X=X_combined_petal_standard
,y=Y_combined_petal
,param_name='C'
,param_range=C_param_range
)
train_petal_mean = np.mean(train_petal_scores,axis=1)
train_petal_std = np.std(train_petal_scores,axis=1)
test_petal_mean = np.mean(test_petal_scores,axis=1)
test_petal_std = np.std(test_petal_scores,axis=1)
plt.subplot(2,2,2)
plt.plot(C_param_range
,train_petal_mean
,color='blue'
,marker='o'
,markersize=5
,label='training acuracidad')
plt.plot(C_param_range
,test_petal_mean
,color='green'
,marker='x'
,markersize=5
,label='test acuracidad')
plt.title('Curva validación para PETALOS')
plt.xlabel('C_parametro')
plt.ylabel('Acuracidad')
plt.legend(loc='lower right')
plt.ylim([0.5,1])
(0.5, 1)
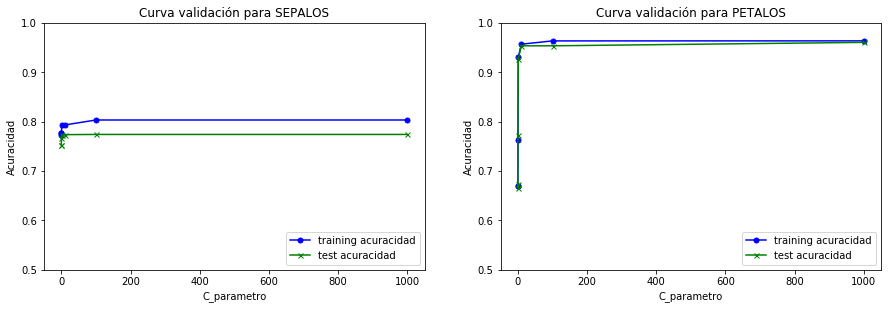
Como puede verse la acuracidad en casi todos los casos es mayor para los PETALOS que para SEPALOS. En resumen, la idea es elegir C de manera que exista la menor diferencia posible entre el conjunto de datos train y test.
